Wird die Quantentechnologie in der Lage sein, Prozesse – wie den Erwartungen entsprechend – zu beschleunigen? Dies hängt maßgeblich davon ab, wie gut Quantenalgorithmen aus dem Lehrbuch mittels spezifischer Hardware-Modelle und -Simulationen an die noch unvollkommenen Quantengeräte angepasst werden können.
Werden Hochleistungsrechner jemals den Quantensprung schaffen? Das Potenzial ist groß: Rein theoretisch könnten Quantencomputer die Prozesse in so unterschiedlichen Bereichen wie Chemie, Materialwissenschaft, Kryptografie und Data Science beträchtlich beschleunigen. Leider haben Quantengeräte inhärente Einschränkungen, die diesen Beschleunigungsprozess unterminieren oder sogar zunichtemachen können. Diese Einschränkungen müssen deshalb bei der Leistungsbeurteilung von Quantencomputern berücksichtigt werden und sie lassen sich sogar nutzen, um die Leistung zu verbessern.

Quantencomputer sollten zunächst für die Lösung von Problemen in der Quantenphysik eingesetzt werden, beispielsweise um herauszufinden, wie sich Quantenteilchen wie Elektronen innerhalb eines Moleküls beim Synthetisieren eines neuen Medikaments verhalten. Forscher entdeckten überraschenderweise schon bald darauf mögliche Einsatzszenarien für die Lösung von Rechenproblemen, die nicht das Geringste mit der Quantenwelt zu tun hatten. Dies trifft beispielsweise auf die für Verschlüsselungssysteme essentielle Faktorisierung großer Zahlen zu. Der Mathematiker Peter Shor zeigte auf, dass Rechenaufgaben mit einem hypothetischen Quantencomputer exponentiell schneller gelöst werden könnten als mit den besten gängigen Algorithmen.

Quanteneigenschaften: exponentielle Leistungssteigerungen – unter Vorbehalt

Um zu verstehen, wie solche Steigerungen möglich sind, sehen wir uns ein zentrales Element des Shor-Algorithmus genauer an: die Fourier-Transformation. Shor reduzierte das Faktorisierungsproblem auf die Bestimmung der Periode einer Funktion, die sich wiederum mithilfe der Fourier-Transformation lösen lässt. Er schlug vor, eine Quantenversion der Fourier-Transformation zu verwenden – anstatt der sogenannten schnellen Fourier-Transformation (Fast Fourier Transform – FFT), dem schnellsten Fourier-Algorithmus auf einem klassischen Computersystem. Während die schnelle Fourier-Transformation etwa „P x log P“-Rechenoperationen für ein Signal der Größe P („log P“ bezeichnet den Logarithmus von P) benötigt, kommt die Quanten-Variante mit nur „log P x log P“ Rechenoperationen aus – eine exponentielle Beschleunigung.

Im Grunde basiert diese Beschleunigung auf zwei Quanteneigenschaften: der Superposition und der Verschränkung. Während sich die möglichen Zustände klassischer Bits auf 0 und 1 beschränken, kann ein Quantenbit (kurz Qubit) auch irgendwo dazwischen liegen, d. h. in einer linearen Kombination oder Superposition von 0 und 1, mit zwei (komplexen) Koeffizienten zur Quantifizierung ihres Stellenwerts. Ebenso können sich N Qubits in Superposition von allen möglichen klassischen Zuständen der N-Bits befinden. Für drei Qubits ergibt sich zum Beispiel eine Superposition von acht (=2³) Zuständen: 000, 001, 010, 011, 100, 101, 110 und 111. Ein Quantenzustand enthält demzufolge Informationen, die 2^N-komplexen Zahlen entsprechen. Im Gegensatz zu klassischen Bits lässt der Gesamtzustand von N Quantenbits nicht auf den Zustand jedes einzelnen Bits schließen – eine Quanteneigenschaft, die Verschränkung genannt wird. Diese exotische Eigenschaft lässt sich auch andersherum einsetzen: Ein Signal, das P Zahlen enthält, kann durch exponentiell weniger Quantenbits, also log P Qubits, beschrieben werden. Das gibt uns bereits einen Hinweis auf die Ursache der exponentiellen Beschleunigung: Während sich der klassische Algorithmus bei Daten einer bestimmten Größe anwenden lässt, manipuliert der Quantenalgorithmus exponentiell kleinere Daten.

Es ist jedoch nicht ohne Weiteres möglich, Nutzen aus diesen exponentiellen Geschwindigkeitsvorteilen zu ziehen. Denn Quantenzustände können nicht genauso einfach gemessen werden wie klassische Zustände. Eine Quantenmessung ist probabilistisch und destruktiv: Sie gibt nur einen der 2^N-klassischen Zustände mit einer Wahrscheinlichkeit wieder, die proportional zur Quadratnorm ihres Koeffizienten ist, und projiziert (und reduziert somit) das Ausgangssignal automatisch auf seinen klassischen Zustand. Um alle Koeffizienten des Ausgangssignals zu erfassen und ein Histogramm der Zustandswahrscheinlichkeiten zu erhalten, müsste die Quanten-Fourier-Transformation deshalb viele Male durchgeführt werden. Dadurch würde der bereits erwähnte erzielte Vorteil stark verringert oder sogar aufgehoben. Um den exponentiellen Geschwindigkeitsvorteil zu nutzen, müssen Wissenschaftler im Bereich Quantum-Computing deshalb intelligente Wege finden, um die im Register enthaltenen Quanteninformationen zu nutzen ohne sie tatsächlich zu messen – oder ein Ausgangssignal konstruieren, das mit wenigen Messungen ausgelesen werden kann.

Diese Programmiereinschränkungen (sowie unzählige weitere kontraintuitive Regeln) weichen radikal von den klassischen Programmierparadigmen ab. Die Quanten-Softwareentwicklung benötigt deshalb geeignete Tools, um sich diese merkwürdigen Eigenschaften zunutze zu machen. Dieser Punkt trifft auch auf die grundlegende Umsetzung eines Quantenschaltkreises zu: Die Quantengatter wirken auf die Quantenbits ein und modifizieren so den Zustand des Quantenregisters. Diese Gatter unterscheiden sich von den klassischen Logikgattern: Sie müssen beispielsweise unitär sein, wodurch das Quantenbit nicht kopiert werden kann. Gemeinsam mit den Quantenmessungen bilden sie eine Sequenz, die als Quantenschaltkreis bezeichnet wird (Abb. 1). Dieser Punkt trifft jedoch auch auf höherer Ebene zu: Die meisten Quantenalgorithmen, wie beispielsweise der Shor-Algorithmus, bestehen aus eindeutigen Unterroutinen (z.B. der Quanten-Fourier-Transformation). Genau wie bei der klassischen Softwareentwicklung benötigen Wissenschaftler im Bereich Quantum-Computing nicht nur Bibliotheken, die vorgefertigte Ausführungen allgemeiner Quantenroutinen zur Verfügung stellen, sondern auch höhere Programmiersprachen, um die Kombination und die mögliche Wiederholung unterschiedlicher Unterroutinen in einem vollständigen Algorithmus zu beschreiben.

Zu guter Letzt müssen Quantenentwickler, da es noch keine fehlerfreien Quantencomputer gibt, dazu in der Lage sein, das Verhalten neuer Quantenalgorithmen auf klassischen Computern zu testen. Nur so lässt sich gewährleisten, dass sie das gewünschte Ergebnis erzielen. So einfach sich das anhört, wird diese Aufgabe doch stark durch die exponentiellen (2^N) Speicheranforderungen beim Speichern eines Quantenzustands auf einem klassischen Computer eingeschränkt.

Zwei Herausforderungen: Quantenkompilierung und Hardware-Einschränkungen

Experimentelle Quantengeräte enthalten eine ganze Reihe hardwarespezifischer Einschränkungen und Fehler. Die gerade genannten Tools sind deshalb wichtig, aber bei weitem nicht ausreichend, um die tatsächliche Leistung eines Quantenalgorithmus zu bewerten und möglicherweise zu verbessern.

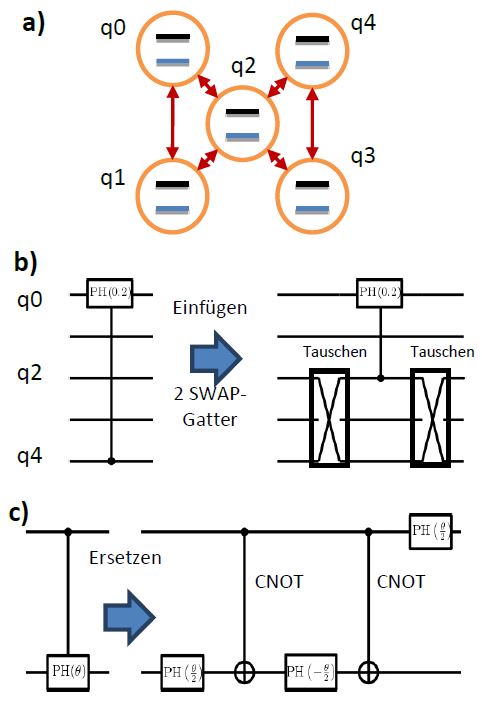
Hardware-Einschränkungen lassen sich mithilfe eines Prozesses namens Kompilierung in den Griff bekommen. Die physikalische Umsetzung eines Quantenprozessors besteht aus Matrizen von Quantenbits, die in einer oder zwei Dimensionen angeordnet sind, wobei jedes Qubit eine beschränkte Anzahl von Nachbarn hat (Abb. 2a). Bei den meisten Ausführungen können 2-Qubit-Gatter nur zwischen benachbarten Qubits angewendet werden. Lehrbuchmäßige Algorithmen wie die oben genannte Fourier-Transformation übersehen diese topologischen Einschränkungen gerne und wenden Gatter zwischen nicht benachbarten Qubits an. Ein Quantenkompilierer muss deshalb den lehrbuchmäßigen Quantenschaltkreis entsprechend umschreiben und die topologischen Einschränkungen berücksichtigen. Dies beinhaltet das Einfügen sogenannter SWAP-Gatter, die den internen Zustand zweier Qubits vertauschen (Abb. 2b). Und während lehrbuchmäßige Algorithmen eine große Anzahl unterschiedlicher Quantengatter enthalten, verfügt jedes Quantengerät aufgrund physikalischer Einschränkungen nur über eine limitierte Anzahl von Gattern. Der Quantenschaltkreis aus dem Lehrbuch muss in einen hardwarespezifischen Gattersatz übersetzt werden (Abb. 2c).

Das Umschreiben bringt Nachteile mit sich: Der Quantenschaltkreis und damit auch die Laufzeiten werden für gewöhnlich wesentlich länger, was zu einer vermehrten Anfälligkeit für Hardwarefehler führen kann. Die Kompilierung muss deshalb unter Einschränkungen optimiert werden, indem beispielsweise die Zahl der Gatter oder die Tiefe des Schaltkreises reduziert wird. Dies stellt an sich schon ein schwieriges Rechenproblem für klassische Computer dar. Es finden derzeit deshalb umfangreiche theoretische und numerische Anstrengungen statt, um effiziente, hardwarespezifische Optimierungsverfahren zu entwerfen.

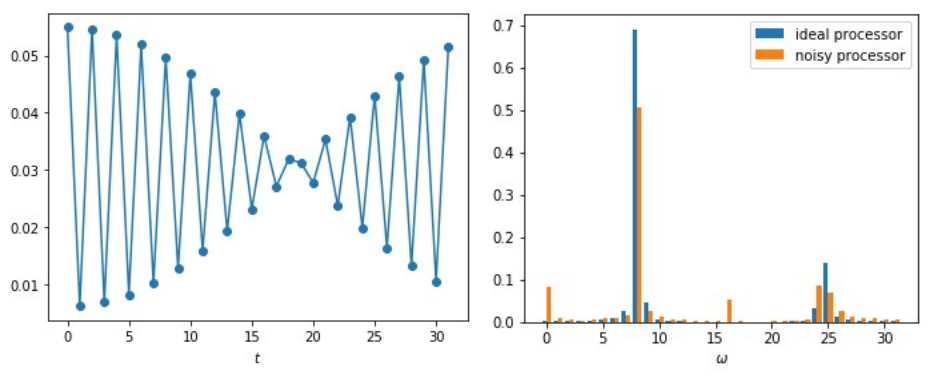
Quantenzustände sind sehr störanfällig. Jede unerwünschte Wechselwirkung mit der Außenwelt kann die Quantenberechnung auf mehrere Arten stören. Dadurch verliert der Quantenzustand aufgrund eines Phänomens namens Dekohärenz allmählich seine Quantenartigkeit, oder die Gatter werden aufgrund unzureichender Kontrolle falsch angewendet. Diese Fehler werden auch als Quantenrauschen bezeichnet und reduzieren die Genauigkeit des Quantencomputers (Abb. 3). Diese Ergebnisse experimentell zu optimieren ist zeit- und kostenintensiv. Mithilfe numerischer Simulationen lassen sich mehr Möglichkeiten untersuchen. Dafür muss zuerst eine brauchbare mathematische Beschreibung der Hardware erstellt werden, die dann auf einem klassischen Computer simuliert wird, um schließlich geeignete Optimierungs- oder Mitigationsstrategien zu entwickeln. Alle drei Schritte stellen schwierige Forschungsprobleme dar. Der erste Schritt besteht in der Identifizierung der relevanten Parameter, um eine bestimmte Art Quanten-Hardware so präzise und so einfach wie möglich zu charakterisieren. Der zweite Schritt ist die Simulation der entsprechenden quantenmechanischen Gleichungen des Modells mit einem klassischen Computer. Dafür sind für gewöhnlich fortgeschrittene numerische Methoden wie die Monte-Carlo-Simulation erforderlich sowie umfassende klassische Computerressourcen.

Anhand eines Abgleichs zwischen den so erzielten numerischen Ergebnissen und den experimentellen Tatsachen kann schließlich ein realistisches Hardware-Modell erstellt werden. Dieses Modell kann dann für die Durchführung des dritten Schrittes eingesetzt werden: die Optimierung des Quantenschaltkreises. Lässt sich beispielsweise die „Qualität“ eines jeden Gatters einer bestimmten Hardware präzise bestimmen, kann ein Quantenschaltkreis kompiliert werden, der die maximale Anzahl qualitativ hochwertiger Gatter enthält. Ebenso kann für den Fall einer mit längerer Laufzeit zunehmenden Dekohärenz ein Schaltkreis kompiliert werden, bei dem die Gesamtlaufzeit des Schaltkreises reduziert wird.

Kurz zusammengefasst: Künftige Quantenprogrammierer müssen nicht nur dazu in der Lage sein, die Richtigkeit von Quantenalgorithmen in einem idealen, fehlerfreien Quantensimulator zu verifizieren. Sie müssen auch das entsprechende Quantenprogramm für eine bestimmte, normalerweise fehlerhafte Hardware simulieren und optimieren. Nur durch diesen Debugging-Prozess sowie durch grundlegende technologische Fortschritte bei den Geräten selbst können wir echte praktische Fortschritte im Bereich der Quantentechnologie erzielen.