Der generelle Ansatz
Was kennzeichnet das Spezifische der visuellen Informationsverarbeitung eines biologischen Gehirns? Das Gehirn rechnet nicht, obwohl sich selbst ordnende Prozesse im Gehirn algorithmisch simuliert werden können. Vielmehr erfasst es die gesamte Musterung bzw. die holistische Form eines Inputs. Das überschreitet derzeit noch die Fähigkeiten eines neuronalen Netzes: das biologische neuronale Netz erzeugt geordnete emergierte Zustände – Aktivitätsmuster, Topologien –, die eine komplexe Information repräsentieren.
So analysiert das biologische neuronale Netz nicht Pixel für Pixel, sondern erfasst das ganze Perzept auf einmal – das nannte die klassische Philosophie „Intuition“. Als Beispiel für Intuition wurden etwa die Identifizierung eines ganzen Musikstücks anhand eines kurzen Ausschnittes oder der „Aha“-Effekt beim mathematischen Problemlösungsprozess, also beim Erfassen der komplexen Information, genannt. Dank Roger Penrose (1964) gibt es auch eine mögliche Veranschaulichung der holistischen Information – hier: der sog. Garben-Kohomologie, das sog. Tribar bzw. Penrose-Dreieck[1]:
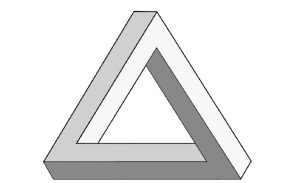
Man erkennt, dass auf der unteren Skala der einzelnen Pixel des Dreiecks jedes Element mit jedem anderen Element konsistent verbunden ist. Nur auf der höheren – holistischen – Skala emergiert eine nicht mehr konsistente Struktur. Die Inkonsistenz kann nur bezogen auf das ganze Perzept konstatiert werden. Die komplexe Information beinhaltet einen zusätzlichen emergierten Informationsgehalt, der ausschließlich holistisch und topologisch kodiert ist.
Wie erfolgt die Enkodierung der einlaufenden Information? Reicht dafür ein klassisches neuronales Netz aus, das immer neue emergente Zustände generiert? Oder bedarf es zwecks Emergenz eines Quanten-Netzes, das parallel zum klassischen Netz die Information verarbeitet und zurück auf das neuronale Netz wirkt (reverse Feedback)? Wie könnte ein hinreichend komplexes Quantennetz durch Setzen der räumlichen und zeitlichen Rahmenbedingungen, d.h. durch kontrollierte Emergenz erzeugt werden? Kann ein Quantensystem verschiedene Stufen der Komplexität physikalisch realisieren? Wäre das ein Rezept gegen Dekohärenz und Dissipation des Quantensystems, das sich durch Zunahme der Komplexität immer mehr selbst stabilisiert, indem es die physikalische Wirkung (als Produkt aus Energie und Zeit) minimiert? Wie viele Schichten der Komplexität müsste ein Quantensystem haben, das bestimmte Aufgaben wie etwa das autonome Autofahren lösen kann? Welche Definition der Quanten-Komplexität wäre dabei erforderlich?
Blicken wir auf das Gehirn höherer Säuger: es operiert nach spezifisch biologischen Prinzipien[2]. So erfolgt die parallele Verarbeitung der Information in neuronalen Ensembles, d.h. auf einer Makro-Skala. Sie bilden emergente Zustände kollektiver neuronaler Erregung. Eine synchrone neuronale Aktivität bildet einen Verarbeitungs- und Repräsentationsschritt der einlaufenden Information, wobei nach Mario Spitzer beim Menschen etwa 23-27 Verarbeitungsschritte aufgeschaltet sind. Zwischen den kollektiven neuronalen Erregungszuständen besteht eine refraktäre Phase der neuronalen Unerregbarkeit. Ob in dieser Phase parallel zur klassischen Informationsverarbeitung eine „reine“ Quanten-Informationsverarbeitung stattfindet, ist Gegenstand von begründeten Spekulationen, um insbes. die Geschwindigkeit, Energieeffizienz, die Komplexität und Ordnung der Informationsverarbeitung zu erklären.
Im biologischen neuronalen Netz erfolgt die Informationsverarbeitung topologisch: der Informationsfluss auf der basalen Ebene der interneuronalen Erregungsleitungsbahnen führt zur Emergenz von solchen Aktivitätsmustern, die durch neuronale Ensembles repräsentiert und generiert werden. Werden die 23-27 nachgeschalteten Erregungsmuster, die zur Verarbeitung eines Perzepts gehören, in ihrer sequentiellen Summe betrachtet, so können sie ihrerseits als analoge Projektionen eines (höher-dimensionalen?!) komplexen Musters interpretiert werden, das verarbeitet wird. Falls die These von der parallel ablaufenden Quanten-Informationsverarbeitung zutrifft, so wäre nur ein Teil dieses komplexen Musters in Form der messbaren neuronalen Aktivität realisiert. Um die ganze komplexe (Quanten-)Information vollständig zu erfassen, bedarf es der Definition eines mathematischen Raums der komplexen Information. Dieser komplexe Möglichkeitsraum enthält sämtliche mögliche komplexe Information, der die einlaufenden Informationen zugeordnet werden können.

Die Zuordnung der einlaufenden Information erfolgt im komplexen Möglichkeitsraum nun durch sich selbst („geordnete Selbstorganisation“). Bei der komplexen Informationsverarbeitung definiert also der komplexe Möglichkeitsraum einen „zentralen Ordner“ (Werner Heisenberg[3]), um die Erzeugung geordneter Muster passiv zu ermöglichen.
Um die o.g. Energieeffizienz und hohe Geschwindigkeit des Quantum Computings[4] auch in einem Quantennetz nutzen zu können, muss dieses komplex genug sein und mindestens beide genannte Schichten der Komplexität physikalisch realisieren. Ohne eine quantenbasierte Künstliche Intelligenz wäre ein klassisches neuronales Netz oder ein klassischer Supercomputer zu langsam, um in Echtzeit komplexe adaptive Leistungen zu vollbringen. Ohne ein komplexes Quantensystem wiederum würde ein binär basiertes Quantum Computing nur eine bestimmte Klasse von mathematischen Problemen schnell lösen können; ein nicht komplexes mehrschichtiges Quantensystem wird daher wohl nie zu einem universalen Quantencomputer!

Das parallel operierende komplexe Quantensystem bildet parallele Rechnerarchitekturen und Topologien in Form einer Quanten-Topologie ab, so wie das ansatzweise beim topologischen Quantum Computing (v.a. IBM) versucht wird[5]. Eine photonisch realisierte topologische Quanteninformationsverarbeitung löst bekanntlich auch die Dekohärenz-Problematik. Da ein komplexer Quantenzustand die komplexe Information repräsentiert, wird ferner eine der Thermodynamik entgegen gerichtete Ordo-Dynamik postuliert, die unten in ihren Grundzügen skizziert wird. Entsprechend der heisenbergschen Energiefunktion wäre hier das Wesentliche die Minimierung der Wirkung als Produkt von Energie und (nicht newtonscher, sondern relativistischer) Zeit durch die Maximierung der informationellen Komplexität.
Transformation von Bits zu QuBits und V-Bits
Um die Geschwindigkeits- und Energievorteile der Quanteninformationsverarbeitung zu nutzen, muss sie physikalisch implementiert werden. An dieser Stelle verweisen wir auf entsprechende Literatur[6] zu neuromorphen Netzen und zur Präparation von Quantenzuständen an Quantenpunkten (quantum dots) eines neuronalen Netzes. Die Quantenpunkte könnten durch sog. Phononen miteinander verschränkt werden[7].
Um die verschiedenen Komplexitätsskalen des klassischen Netzes abzubilden, sollten auch im Quantensystem verschiedene Komplexitätsskalen emergieren – bislang wurde das leider noch nicht in einem Labor realisiert. Eine sich (relativ) selbst vollziehende Emergenz komplexer Information wäre eine (An-)Ordnung von Qubits, die nach ihrer artifiziellen Initiierung durch die räumliche Positionierung und zeitliche Aktivierung der Quantenpunkte in der Lage wäre, sich selbst zu ordnen und dadurch zu stabilisieren. Sobald das komplexe Quantensystem initiiert wäre, könnte es „ordnend“ zurück auf die räumliche Positionierung und zeitliche Aktivierung der Neuronen wirken (reverses Feedback)[8]. Somit würde das klassische komplexe System die Emergenz des Quantensystems raumzeitlich koordinieren – und umgekehrt!

Somit könnte – so unsere These – das klassische Muster analog in eine komplexere (!) Quanten-Topologie übersetzt werden. Dabei emergieren im Quantensystem beide genannten Hierarchien von Topologien mit unterschiedlicher Informationsdichte. Die erste Stufe der Emergenz wäre die o.g. Zuordnung der erfassten Perspektive des informatorischen Inputs zu einem Perzept, und die zweite Stufe der Emergenz entspricht dann der Zuordnung dieses Perzepts zur o.g. Klasse von äquivalenten Perzepten. Jeder Emergenz-Stufe entspricht eine eigene komplexe Topologie.
Bezogen auf die Zunahme an Komplexität kann das durch eine Pyramide veranschaulicht werden. Die maximale synergetische Informationskompression wäre an der Spitze einer „Quante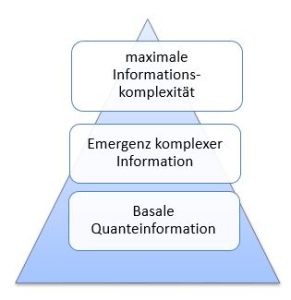
Präparation und Verschränkung
Folgende Stichpunkte fassen skizzenhaft den postulierten Prozess der emergierenden Quanten-Informationsverarbeitung zusammen[9]:
- Koordinierte Präparation von QuBits (Hadamard-Gates) an selektierten Quantenpunkten (quantum dots);
- Verschränkung der QuBits durch Phononen oder Photonen zu sog. V-Bits (=Verschränkungs-Bits). Die V-Bits repräsentieren einen Produktzustand, der über die quantenmechanische Superposition hinaus instantane informationelle Wechselwirkung (unterhalb der Bell-Grenze) erlaubt;
- Verschiedene V-Bits zu Meta-V-Bits verschränkt ergeben schließlich ein makroskopisches komplexes Quantensystem (=MCQS). MCQS ist die Bedingung der Möglichkeit der physikalischen Implementierung einer holistischen Information, die sämtliche Quantenpunkte des neuromorphen Netzes umfasst und sämtliche basale Information integriert;
- MCQS sollen nun die physikalische Realisierung der sog. komplexen Information Die komplexe Information kann topologisch als spezifisches Muster beschrieben werden, das im Quantennetz realisiert ist. Dieses Quanten-Muster speichert den eingehenden Input durch die Bildung spezifischer Quanten-Produktzustände;
- erfolgt eine damit implizierte holografische Speicherung in Anlehnung an die Fourier-Transformation, um keine einzelnen „Zahlen“, sondern um „Funktionen“ zu speichern: f(x)=

- Die dynamische Verarbeitung der komplexen Information geschieht dann durch Transformationen der komplexen Information unter Wahrung derselben Komplexitätsklasse, die der komplexe Möglichkeitsraum definiert.
Der komplexe Möglichkeitsraum erfüllt nun folgende Eigenschaften: Er enthält in sich (analog) den Unterraum aller möglichen komplexen Information; er begrenzt den Selektions- und Suchraum der komplexen Information, so dass das System schnell auf den Zielzustand der gesuchten komplexen Information konvergieren kann; er gibt die Regeln bzw. Operatoren der Transformation und Verarbeitung der komplexen Information vor.
Artifiziell erfolgt also die Initiierung eines komplexen Quantensystems, das sich ab dann selbst ordnen und die Aktivierung bzw. Inaktivierung von Quantenpunkten i.S. der quantenmechanischen „Messung“ koordinieren bzw. ordnen soll. Das Hybrid-System aus dem klassischen neuronalen und dem Quantennetz wäre in der Lage, sich an verschiedene visuelle Inputs anzupassen, wobei das (nicht überwachte) Resultat der Anpassung die gesuchte komplexe Information wäre.
Wie könnte der komplexe Möglichkeitsraum definiert werden? Hier kann derzeit nur spekuliert werden. Könnte etwa anstatt eines Basisvektors und seinem Skalar über ein Basis-Fraktal oder Basis-Kristall und seinen analogen Projektionsoperator nachgedacht werden?[10] Dann wäre der komplexe Möglichkeitsraum sowohl „körnig“ bzw. quantisiert als auch begrenzt. In der physikalischen Realität gibt es keine mathematischen Unendlichkeiten, daher bedarf es einer prinzipiellen Begrenzung der Möglichkeiten, komplexe Zustände bzw. eine komplexe Information zu verwirklichen. Ein komplexer Zustand könnte etwa das Tensorprodukt von Basis-Kristallen oder Basis-Fraktalen in dem Raum sein, den sie aufspannen. Die Quantisierung dieses komplexen Möglichkeitsraums erlaubt ferner, die Nichtlinearität der Veränderung einer komplexen Information abzubilden. Ab einem Schwellenwert könnte diese Veränderung als Phasenübergang definiert werden: durch nichtlineare Transformation könnte eine Information von höherer Komplexität und Mächtigkeit und somit eine neue Komplexitätsschicht emergieren. An der mathematischen Beschreibung wird derzeit gearbeitet.
Ordo-Dynamik
Der Definition von Ordnung in Abhebung von Unordnung dient die im Folgenden skizzenhaft vorgeschlagene Ordo-Dynamik. Verschiedene prinzipielle Annahmen fließen in eine noch im Detail auszuarbeitende Theorie der Ordo-Dynamik ein[11]:
- Stabilisierung des Quantensystems durch Zunahme der Ordnung (Neg-Entropie) und Abnahme der Wirkung (Minimierung der physikalischen Wirkung). Die physikalische Wirkung wird, so das Postulat, dadurch minimiert, dass sie teilweise in eine informationelle Wirkung transformiert wird[12]. Dabei soll die gesamte Wirkung als Produkt der informationellen und physikalischen Wirkung erhalten bleiben:

- Bezogen auf Quantensysteme muss ein nicht-klassischer Begriff der (Wechsel-)Wirkung vorausgesetzt werden – bereits Einstein spricht für den Fall von verschränkten Quantenzuständen von einer „Wechselwirkung“[13]. Eine Quanten-Wirkung jedoch hat einen primär informationellen Charakter, wobei aufgrund des Non-Cloning-Theorems der Begriff der „Information“ keine klassische Information meint, sondern eine Verschränkungs-Information (V-Bit). Ein V-Bit als „besonderer“ Produktzustand von QuBits entspricht einer informationellen Quanten-Wechsel-Wirkung einer bidirektionalen Relation.
- Relationen wiederum ordnen QuBits ähnlich wie die Anordnung von Buchstaben ein sinnvolles Wort ergibt. Insofern V-Bits eine Anordnung bzw. Information unterschiedlicher Komplexität und Ordnung repräsentieren, muss der Raum der erlaubten und möglichen V-Bits durch den komplexen Möglichkeitsraum begrenzt sein.
- Ferner wird die makroskopische Relevanz von Quanteneffekten gemäß des Diktums von Erwin Schrödinger postuliert: aus einer Quanten-Ordnung erfolgt makroskopische (raumzeitliche) Ordnung (1944) – und umgekehrt[14]. D.h. ein biologisches System probiert – im Unterschied zu anorganischen Systemen – verschiedene (An-)Ordnungsmöglichkeiten im (begrenzten) komplexen Möglichkeitsraum aus.
- Der Begriff der Entropie könnte differenziert definiert werden, um auch bestimmte komplexe Anordnungen als unmöglich auszuschließen. Die thermodynamische Dissipationsskala eines Quantensystems hängt mit der davon unterschiedenen Dekohärenzskala zusammen, was die Ableitung der Entropie aus einem veränderten Enthalpie-Begriff nahelegt, die ihrerseits aus einem anderen Begriff der Wirkung (und Wirklichkeit) von Quantensystemen und –zuständen resultiert.
Diese im Detail zu klärenden Annahmen vorausgeschickt, kann nun der Versuch unternommen werden, ein Postulat der Ordo-Dynamik komplexer Systeme zu formulieren. IE sei die informationelle Energie, H1 die erste Komologie-Gruppe (als mögliche Definition der komplexen Information CI):

Eine Alternative setzt an der Analogie an, die ein universales Prinzip aller Ordnung ist. Die Analogie wird mathematisch ausgedrückt durch die irrationale Zahl φ. Der goldene Schnitt φ wurde in der Philosophie als sog. attributive Analogie ausgedrückt:
A:B = B:C
Ihr könnte eine irrationale Funktion zugeordnet werden. Das legt die Annahme nahe, dass φ die Zahl der Möglichkeiten, Ordnung anzunehmen, begrenzt und daher wesenhaft in die o.g. Definition des komplexen Möglichkeitsraums eingeht. Auch quantenphysikalisch geht bekanntlich φ in einer fundamentalen Weise in die Definition von unitären Operatoren ein. Damit legt sich der Schluss nahe, dass die Wirklichkeit analog strukturiert ist und seine kleinsten Wirkungseinheiten die Signatur der Analogie bzw. Ordnung an sich tragen.
Unabhängig davon lässt sich die informationelle Wirkung in ordo-dynamischen Systemen physikalisch als geordnetes V-Bit auffassen und definieren als:
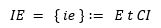
Die Neg-Entropie 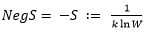
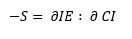
Die Negentropie in komplexen Systemen nimmt dabei nicht ab, sondern ist äquivalent zu: 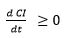
Die Neg-Enthalpie –H wiederum wird, ohne dabei auf den ontologischen Modus der Wirkung und Wirklichkeit eines Quantensystems einzugehen, definiert als:
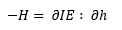
Damit beschreibt die Ordo-Dynamik, dass in der Evolution offene thermodynamische Systeme unter Energieverbrauch zu komplexeren Strukturen und Mustern als Verwirklichungen immer komplexerer Information streben. Dabei lagern sie Entropie an eine „Außenwelt“ ab, was eine Brechung der internen Symmetrie des Systems bedeutet. Parallel dazu nimmt eine „komplexe“ Symmetrie zu, die die komplexe Information CI kennzeichnet:
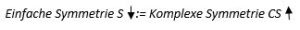
Ein bestimmtes Grad an komplexer Symmetrie definiert topologisch eine Gruppe von periodischen Mustern, d.h. mathematisch ein komplexes Kristall. Dieses wird einer Schicht der komplexen Information bzw. Topologie im Quantensystem zugeordnet. Sie wird definiert durch den komplexen Möglichkeitsraum.
Innerhalb der dadurch definierten möglichen Systemzustände sollen nun diejenigen Zustände selektiert werden, die eine CI koordiniert emergieren lassen. Liegt die CI, wie hier vorgeschlagen, als komplexes Quantensystem vor, so bedeutet eine kontrollierte und künstlich geordnete Emergenz von CI an Quantenpunkten (q dots), dass diese Quantenpunkte räumlich vernetzt und zeitlich geordnet aktiviert werden müssen. Die CI wirkt durch informationelle Energie: die Information löst dann eine Aktivierung oder Inaktivierung eines q dots koordiniert aus. Es werden verschiedene q dots zu Gruppen G (q dots) zusammen gefasst, und diese Gruppen wiederum zu Gruppen G` von größerer informationeller Mächtigkeit als Repräsentationen der jeweiligen Komplexitätsschicht.
Die Zusammenfassung und Ordnung der einlaufenden Information geschieht durch Erfassung der Ordnung der raumzeitlichen Relationen der q dots sowie der Gruppen von q dots, d.h. durch Enkodierung ihrer Relationen i,j:
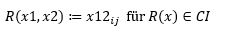
Dadurch bildet sich ein raumzeitliches Muster M. Dieses Muster M ist selbstähnlich und nicht selbst-identisch, weil es sich analog auf verschiedenen Skalen wiederholt bzw. abbildet:
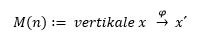
Das Muster M ist ein Bestandteil des komplexen Möglichkeitsraums R(CI):
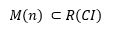
Bezogen auf die physikalische Wirkungsminimierung gilt: das Produkt aus Wirkung und der Kopplungskonstanten der q dots ist somit abhängig vom Wirkungsradius r der jeweiligen Ordnungsskala bzw. Komplexitätsschicht. Die Relationen R sind dabei abhängig vom goldenen Schnitt φ (=topologische Definition auf Basis der sog. analogen Projektion).
Um nun die Dynamik der Ordnung zu erfassen, kann die Veränderung des Musters M in Abhängigkeit von Ort und Zeit begriffen werden:
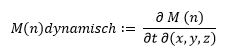
Die Emergenz von holistischer Ordnung
Wie entsteht nun konkrete Ordnung in lebendigen Systemen statt eines Chaos? – Durch den o.g. „zentralen Ordner“ bzw. durch den komplexen Möglichkeitsraum. Er trennt gewissermaßen die Ordnung vom Chaos, indem es die Anzahl der Möglichkeiten der Emergenz bzw. der Selbst-Ordnung begrenzt. Die Dynamik der komplexen Informationsverarbeitung geschieht in diesem komplexen Möglichkeitsraum. Ohne eine solche Vorgabe eines komplexen Möglichkeitsraums (in Entsprechung zu den eingangs genannten Schemata) wäre eine geordnete Selbstorganisation nicht möglich.
Warum bedarf es überhaupt einer komplexen Ordnung in einem Quantensystem? Weil der komplexen Information ein mehrschichtiges System entsprechen soll (sog. Schichtenmodell) und weil so die entscheidenden Vorteile der Quanteninformationsverarbeitung (Geschwindigkeit, Energie-Effizienz, ultraschnelle Parallelverarbeitung, physikalische Realisierung komplexer Information) genutzt werden können. Ohne ein mehrschichtiges komplexes Quantensystem als analoges Korrelat eines neuronalen Netzwerks ist es schwer vorstellbar, wie die komplexe Informationsverarbeitung physikalisch implementiert werden kann.
Anhand eines Präparationsvorgangs von QuBits und V-Bits an künstlich platzierten Quantenpunkten sollte daher ein mehrschichtiges komplexes Quantensystem entstehen. Die komplexen (fraktalen?!) Aktivierungsmuster, die zur Initiierung des hybriden neuronalen Netzes führen, könnten durch eine Vorschrift erzeugt werden, die der folgenden fraktalen Funktion genügt:
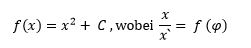
Das hybride System soll etwa beim autonomen Autofahren einer spezifischen Mustererkennung dienen, indem sie die beiden Komplexitätsschichten im Quantensystem emergieren lässt. D.h. das System bildet die physikalische Implementierung des spezifischen komplexen Möglichkeitsraums ab, der die Summe der Verkehrsschilder in Form von komplexer Informationen definiert. Während des Zuordnungsprozesses wird eine komplexe Information CI(n) auf CI(n+1) gemappt bzw. durch Anwendung eines komplexen Operators ineinander transformiert. Welcher Operator angewandt wird, soll Resultat eines Selbstorganisationsprozesses sein und ist nicht durch den komplexen Möglichkeitsraum determiniert.
Wie erwähnt, bildet auch das Quantensystem ein mehrschichtiges Quanten-Netz. Die Verbindungen zwischen QuBits wären die V-Bits. Welche Kombination bzw. Anordnung von V-Bits ist nun erlaubt? Hier ist es hilfreich, auf den Prozess der Selbstassemblierung zu schauen. Das System organisiert sich selbst in Richtung der gewünschten komplexen Information als Output. Dieser Prozess kann als Bewegung im Raum der möglichen (An-)Ordnungen der QuBits bzw. als Veränderung der Quanten-Topologie bis zur gewünschten Topologie modelliert werden. Dann gilt für die Wahrscheinlichkeit der Bewegung des Systemzustands Z in Richtung der gesuchten komplexen Information CI:
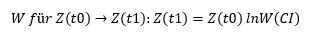
Man beachte: der Prozess der Selbstorganisation ist historisch relevant, d.h. das System besitzt im Unterschied zu einem Markov-Prozess eine historische Spur bzw. ein Gedächtnis, so dass die vergangenen Korrelationen in die zukünftige Entwicklung des Systems konstitutiv mit eingehen.
Durch Synergien soll es nun zur „antriebsabhängigen“ zeitlichen (Synchronizität) und räumlichen (Ensemblebildung) Koordination[15] kommen. Die Synergien, die zu einer CI passen, setzen entsprechende Kopplungsstärken KS voraus. Sie sollte proportional zum Kehrwert der Entropie S mal einer Komplexitätskonstante C sein:
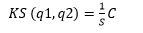
Die Bewegung des Systems approximiert nun den Zustand des Gesamtsystems mit maximaler CI, so dass gilt:
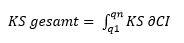
Somit gibt es lediglich eine allgemeine Selektionsregel für das Zustandekommen der gewünschten Synergien, dass CI zunimmt und die Wirkung W in Abhängigkeit von der Komplexitätskonstante C abnimmt:
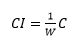
Der Selektionsdruck wird also durch das Prinzip der Minimierung der Wirkung vorgegeben und bestimmt die Wahl des jeweiligen Transformationsoperators. Physikalisch wird ein Teil der Wirkung, die generell als Ansammlung von Information beschrieben werden kann, in komplexe Information zurück-transformiert. Daraus folgt die Abnahme und Auslagerung der Entropie durch Zunahme der Komplexität. Das wiederum führt zur sukzessiven Realisierung immer komplexerer Information.
Definition und Verarbeitung der dynamischen komplexen Information
Der komplexe Möglichkeitsraum bestimmt also die endliche Anzahl der topologischen komplexen Information. Sie hat folgende Eigenschaften:
- Die komplexe Information kann als komplexe (geometrische und algebraische) Topologie verstanden werden
- Die komplexe Information ist holistisch und nichtlokal
- Die komplexe Information ist höher-dimensional und ist eine Untermenge des komplexen Möglichkeitsraums
- Die komplexe Information kodiert die Relationen (zwischen Bits, aber auch zwischen QuBits) und definiert begrenzt somit die Menge möglicher Muster.
Die komplexe Information des 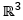
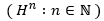
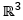
Resümee
Die Untersuchung der höheren Kohomologie-Gruppen 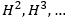
Der Prozess der Rekonstruktion meint im Einzelnen:
- Assoziation der einlaufenden Information mit vorhandener Information: Verbindung und Trennung möglicher Relationen zwischen den Informationseinheiten, die ihrerseits in neuronalen Gruppen bzw. „Modulen“ auf einer gegenüber dem einzelnen Neuron höheren (emergenten) Skala repräsentiert sind.
- Kombination von Informationseinheiten zu emergenten Gruppen, wobei passende Kombinationen positiv selektiert werden. Die Selektion erfolgt also auf der Ebene von komplexen Informationseinheiten bzw. neuronalen Gruppen.
- Der komplexe Möglichkeitsraum gibt dabei die Regeln der Verbindung und Trennung von Relationen an bzw. definiert die möglichen Operatoren, ohne Ihre Aktivierung im einzelnen zu determinieren.
Zur komplexen Informationsverarbeitung stellt sich technologisch u.a. die Frage, welche klassische (An-)Ordnung von q dots zur Emergenz der gesuchten komplexen Information überhaupt geeignet ist. Sobald das erste reverse Feedback erfolgreich gestartet wurde, ordnet sich das System fortan selbst (geordnete Selbstorganisation) wie das biologische neuronale Netz und erzeugt die gewünschten Outputs. Die quantenbasierte topologische komplexe Informationsverarbeitung könnte das physikalische Substrat einer komplexen Informationsverarbeitung darstellen.
Die komplexe Information ist eine holistische und integrative Information, die einerseits das Ergebnis eines Generalisierungsprozesses durch Emergenz ist, andererseits durch vorgegebene Schemata bzw. durch den komplexen Möglichkeitsraum überhaupt erst definiert ist und zustande kommt. So wird im Rahmen einer vorgegeben komplexen Ordnung des komplexen Möglichkeitsraums eine eigene Ordnung kreativ erzeugt! Diese emergente Ordnung ist Resultat von künstlich induzierten Selbstorganisationsprozessen und repräsentiert hochgradig komplexe adaptive Reaktionen und autonom-flexible Aktionen in Echtzeit – ein Meilenstein auf dem Weg zur ersten „echten“ Künstlichen Intelligenz!
Quellen und Referenzen
[1] Roger Penrose: The road to reality. A complete guide to the laws of the universe, New York 2007
[2] Vgl. dazu Wolf Singer: Hirnforschung an den Grenzen der Vorstellungskraft, Müllheim 2019 (eine DVD); Gerhard Roth: Aus Sicht des Gehirns, Berlin 2019 (vollständig überarbeitete Neuauflage)
[3] Werner Heisenberg: Der Teil und das Ganze, Gespräche im Umkreis der Atomphysik, München 2006
[4] Zu diesem zentralen Argument für Quanteninformationsverarbeitung im biologischen Gehirn siehe Thomas und Brigitte Görnitz: Von der Quantenphysik zum Bewusstsein. Kosmos, Geist und Materie, Berlin u.a. 2016. Hier sollte man freilich von der ideologischen Motivation beider Autoren, eine in Anlehnung an C.G. Jung und C.F.v.Weizsäcker propagierte „Protyposis“ auf Basis passend selektierter (!) mathematischer Formalismen der Quantenmechanik absehen.
[5] Jannis K. Pachos: Introduction to Topological Quantum Computing, Cambridge 2012. Siehe auch Steve H. Simon: The Oxford solid state basics, Oxford 2017, der das passende physikalische Substrat für topologisches Quantum Computing sucht.
[6] Vgl. den Überblick in: IX Developer 2018 – Machine Learning: Verstehen, verwenden, verifizieren, Hannover 2018 (Heiser Media, online Ressource).
[7] Martin Schulz: Quantum Dots for Quantum Information Processing: Controlling and Exploiting the Quantum Dot Environment, Berlin u.a. 2017
[8] Der Begriff ist eine Erweiterung des „reverse engineering“: Florian Neukart: Reverse engineering the mind. Consciously acting machines and accelerated evolution, Wiesbaden 2017.
[9] Vgl. einleitend: Imre Koncsik: Unser Gehirn – ein biologischer Quantencomputer? Die verborgene geistige Ordnung, Göttingen 2019. Die „verborgene geistige Ordnung“ soll den hier vorgeschlagenen komplexen Möglichkeitsraum definieren.
[10] Eine Möglichkeit, Basis-Fraktale statt Basis-Simplices zu definieren, bietet sich bei der sog. „kausalen dynamischen Triangulation“ an. Vgl. dazu die kurze Anwendung dieser Methode bei Renate Loll: Taming the cosmological constant in 2D causal quantum gravity with topology change, Aachen 2005.
[11] Einen physikalischen Meilenstein verdanken wir Jeremy England: Statistical Physics of Self-Replication, J. Chem. Phys. 139 (2013) 121923. Hier wird anhand der höheren Anzahl komplexer Zustände im Vergleich zu unterkomplexen Zuständen eine höhere Wahrscheinlichkeit angenommen, die ihrerseits zu einer zeitlichen Gerichtetheit und Irreversibilität der Entwicklung zu mehr Komplexität führt. Zwischen den komplexen Zuständen wird jedoch nicht mehr dahingehend unterschieden, dass nur wenige unter ihnen zur Selbstreplikation führen.
[12] Mit Carl Friedrich von Weizsäcker wird hierbei eine Transformierbarkeit von Energie, Materie und Information postuliert.
[13] Siehe die Darstellung bei Andrew Whitaker: Einstein, Bohr and the quantum dilemma, Cambridge 1996
[14] Das setzt voraus, dass Differenzen auf der subatomaren Skala der Quantenwirklichkeit auf höheren Skalen nicht „gemittelt“ werden, sondern eine makroskopische komplexe Ordnung emergieren (!) lassen. Jim Al-Khalili; Johnjoe McFadden: Der Quantenbeat des Lebens. Wie Quantenbiologie die Welt neu erklärt, Berlin 2015.
[15] Holger Schmid-Schönbein: Erklärung biologischer „Als-ob-Teleonomie“. Startbedingungen determinieren das Ordnen von Lebensvorgängen, in: Koncsik, I.; Wilhelms, G. (Hgg.), Jenseits, Evolution, Geist. Schnittstellen zwischen Theologie und Naturwissenschaften, Frankfurt a.M. 2003, 113-204
[16] Siehe zum Folgenden: Robin Hartshorne: Algebraic Geometry, GTM 52, New York 2010; Richard Ward, Raymond Wells Jr: Twistor geometry and field theory, Cambridge 1995;
[17] Peter Nonnenmann; Imre Koncsik: Topologische komplexe Informationsverarbeitung in neuronalen Netzen, in: Digitale Welt, Ausgabe 4 (2019) 67-69
Quantenbasierte komplexe Informationsverarbeitung
Der generelle Ansatz
Was kennzeichnet das Spezifische der visuellen Informationsverarbeitung eines biologischen Gehirns? Das Gehirn rechnet nicht, obwohl sich selbst ordnende Prozesse im Gehirn algorithmisch simuliert werden können. Vielmehr erfasst es die gesamte Musterung bzw. die holistische Form eines Inputs. Das überschreitet derzeit noch die Fähigkeiten eines neuronalen Netzes: das biologische neuronale Netz erzeugt geordnete emergierte Zustände – Aktivitätsmuster, Topologien –, die eine komplexe Information repräsentieren.
So analysiert das biologische neuronale Netz nicht Pixel für Pixel, sondern erfasst das ganze Perzept auf einmal – das nannte die klassische Philosophie „Intuition“. Als Beispiel für Intuition wurden etwa die Identifizierung eines ganzen Musikstücks anhand eines kurzen Ausschnittes oder der „Aha“-Effekt beim mathematischen Problemlösungsprozess, also beim Erfassen der komplexen Information, genannt. Dank Roger Penrose (1964) gibt es auch eine mögliche Veranschaulichung der holistischen Information – hier: der sog. Garben-Kohomologie, das sog. Tribar bzw. Penrose-Dreieck :
Man erkennt, dass auf der unteren Skala der einzelnen Pixel des Dreiecks jedes Element mit jedem anderen Element konsistent verbunden ist. Nur auf der höheren – holistischen – Skala emergiert eine nicht mehr konsistente Struktur. Die Inkonsistenz kann nur bezogen auf das ganze Perzept konstatiert werden. Die komplexe Information beinhaltet einen zusätzlichen emergierten Informationsgehalt, der ausschließlich holistisch und topologisch kodiert ist.
Wie erfolgt die Enkodierung der einlaufenden Information? Reicht dafür ein klassisches neuronales Netz aus, das immer neue emergente Zustände generiert? Oder bedarf es zwecks Emergenz eines Quanten-Netzes, das parallel zum klassischen Netz die Information verarbeitet und zurück auf das neuronale Netz wirkt (reverse Feedback)? Wie könnte ein hinreichend komplexes Quantennetz durch Setzen der räumlichen und zeitlichen Rahmenbedingungen, d.h. durch kontrollierte Emergenz erzeugt werden? Kann ein Quantensystem verschiedene Stufen der Komplexität physikalisch realisieren? Wäre das ein Rezept gegen Dekohärenz und Dissipation des Quantensystems, das sich durch Zunahme der Komplexität immer mehr selbst stabilisiert, indem es die physikalische Wirkung (als Produkt aus Energie und Zeit) minimiert? Wie viele Schichten der Komplexität müsste ein Quantensystem haben, das bestimmte Aufgaben wie etwa das autonome Autofahren lösen kann? Welche Definition der Quanten-Komplexität wäre dabei erforderlich?
Blicken wir auf das Gehirn höherer Säuger: es operiert nach spezifisch biologischen Prinzipien . So erfolgt die parallele Verarbeitung der Information in neuronalen Ensembles, d.h. auf einer Makro-Skala. Sie bilden emergente Zustände kollektiver neuronaler Erregung. Eine synchrone neuronale Aktivität bildet einen Verarbeitungs- und Repräsentationsschritt der einlaufenden Information, wobei nach Mario Spitzer beim Menschen etwa 23-27 Verarbeitungsschritte aufgeschaltet sind. Zwischen den kollektiven neuronalen Erregungszuständen besteht eine refraktäre Phase der neuronalen Unerregbarkeit. Ob in dieser Phase parallel zur klassischen Informationsverarbeitung eine „reine“ Quanten-Informationsverarbeitung stattfindet, ist Gegenstand von begründeten Spekulationen, um insbes. die Geschwindigkeit, Energieeffizienz, die Komplexität und Ordnung der Informationsverarbeitung zu erklären.
Im biologischen neuronalen Netz erfolgt die Informationsverarbeitung topologisch: der Informationsfluss auf der basalen Ebene der interneuronalen Erregungsleitungsbahnen führt zur Emergenz von solchen Aktivitätsmustern, die durch neuronale Ensembles repräsentiert und generiert werden. Werden die 23-27 nachgeschalteten Erregungsmuster, die zur Verarbeitung eines Perzepts gehören, in ihrer sequentiellen Summe betrachtet, so können sie ihrerseits als analoge Projektionen eines (höher-dimensionalen?!) komplexen Musters interpretiert werden, das verarbeitet wird. Falls die These von der parallel ablaufenden Quanten-Informationsverarbeitung zutrifft, so wäre nur ein Teil dieses komplexen Musters in Form der messbaren neuronalen Aktivität realisiert. Um die ganze komplexe (Quanten-)Information vollständig zu erfassen, bedarf es der Definition eines mathematischen Raums der komplexen Information. Dieser komplexe Möglichkeitsraum enthält sämtliche mögliche komplexe Information, der die einlaufenden Informationen zugeordnet werden können.
Die Zuordnung der einlaufenden Information erfolgt im komplexen Möglichkeitsraum nun durch sich selbst („geordnete Selbstorganisation“). Bei der komplexen Informationsverarbeitung definiert also der komplexe Möglichkeitsraum einen „zentralen Ordner“ (Werner Heisenberg ), um die Erzeugung geordneter Muster passiv zu ermöglichen.
Um die o.g. Energieeffizienz und hohe Geschwindigkeit des Quantum Computings auch in einem Quantennetz nutzen zu können, muss dieses komplex genug sein und mindestens beide genannte Schichten der Komplexität physikalisch realisieren. Ohne eine quantenbasierte Künstliche Intelligenz wäre ein klassisches neuronales Netz oder ein klassischer Supercomputer zu langsam, um in Echtzeit komplexe adaptive Leistungen zu vollbringen. Ohne ein komplexes Quantensystem wiederum würde ein binär basiertes Quantum Computing nur eine bestimmte Klasse von mathematischen Problemen schnell lösen können; ein nicht komplexes mehrschichtiges Quantensystem wird daher wohl nie zu einem universalen Quantencomputer!
Das parallel operierende komplexe Quantensystem bildet parallele Rechnerarchitekturen und Topologien in Form einer Quanten-Topologie ab, so wie das ansatzweise beim topologischen Quantum Computing (v.a. IBM) versucht wird . Eine photonisch realisierte topologische Quanteninformationsverarbeitung löst bekanntlich auch die Dekohärenz-Problematik. Da ein komplexer Quantenzustand die komplexe Information repräsentiert, wird ferner eine der Thermodynamik entgegen gerichtete Ordo-Dynamik postuliert, die unten in ihren Grundzügen skizziert wird. Entsprechend der heisenbergschen Energiefunktion wäre hier das Wesentliche die Minimierung der Wirkung als Produkt von Energie und (nicht newtonscher, sondern relativistischer) Zeit durch die Maximierung der informationellen Komplexität.
Transformation von Bits zu QuBits und V-Bits
Um die Geschwindigkeits- und Energievorteile der Quanteninformationsverarbeitung zu nutzen, muss sie physikalisch implementiert werden. An dieser Stelle verweisen wir auf entsprechende Literatur zu neuromorphen Netzen und zur Präparation von Quantenzuständen an Quantenpunkten (quantum dots) eines neuronalen Netzes. Die Quantenpunkte könnten durch sog. Phononen miteinander verschränkt werden .
Um die verschiedenen Komplexitätsskalen des klassischen Netzes abzubilden, sollten auch im Quantensystem verschiedene Komplexitätsskalen emergieren – bislang wurde das leider noch nicht in einem Labor realisiert. Eine sich (relativ) selbst vollziehende Emergenz komplexer Information wäre eine (An-)Ordnung von Qubits, die nach ihrer artifiziellen Initiierung durch die räumliche Positionierung und zeitliche Aktivierung der Quantenpunkte in der Lage wäre, sich selbst zu ordnen und dadurch zu stabilisieren. Sobald das komplexe Quantensystem initiiert wäre, könnte es „ordnend“ zurück auf die räumliche Positionierung und zeitliche Aktivierung der Neuronen wirken (reverses Feedback) . Somit würde das klassische komplexe System die Emergenz des Quantensystems raumzeitlich koordinieren – und umgekehrt!
Klassischer Zustand Quantenzustand
Somit könnte – so unsere These – das klassische Muster analog in eine komplexere (!) Quanten-Topologie übersetzt werden. Dabei emergieren im Quantensystem beide genannten Hierarchien von Topologien mit unterschiedlicher Informationsdichte. Die erste Stufe der Emergenz wäre die o.g. Zuordnung der erfassten Perspektive des informatorischen Inputs zu einem Perzept, und die zweite Stufe der Emergenz entspricht dann der Zuordnung dieses Perzepts zur o.g. Klasse von äquivalenten Perzepten. Jeder Emergenz-Stufe entspricht eine eigene komplexe Topologie.
Bezogen auf die Zunahme an Komplexität kann das durch eine Pyramide veranschaulicht werden. Die maximale synergetische Informationskompression wäre an der Spitze einer „Quanten-Pyramide“ verwirklicht. Die Dynamik der topologischen Quanten-Informationsverarbeitung vollzieht sich auf der klassischen und der quantischen Ebene parallel, wenn auch auf verschiedenen räumlichen und zeitlichen Skalen. Die Konstruktion der topologischen Muster erfolgt in Anlehnung an Gerald Edelmann gemäß der Theorie der neuronalen Gruppenselektion (TNGS), also nach evolutionstheoretischen Prinzipien einer geordneten (!) – und sich selbst ordnenden –Anwendung von Regeln bzw. Operatoren.
Präparation und Verschränkung
Folgende Stichpunkte fassen skizzenhaft den postulierten Prozess der emergierenden Quanten-Informationsverarbeitung zusammen :
Koordinierte Präparation von QuBits (Hadamard-Gates) an selektierten Quantenpunkten (quantum dots);
Verschränkung der QuBits durch Phononen oder Photonen zu sog. V-Bits (=Verschränkungs-Bits). Die V-Bits repräsentieren einen Produktzustand, der über die quantenmechanische Superposition hinaus instantane informationelle Wechselwirkung (unterhalb der Bell-Grenze) erlaubt;
Verschiedene V-Bits zu Meta-V-Bits verschränkt ergeben schließlich ein makroskopisches komplexes Quantensystem (=MCQS). MCQS ist die Bedingung der Möglichkeit der physikalischen Implementierung einer holistischen Information, die sämtliche Quantenpunkte des neuromorphen Netzes umfasst und sämtliche basale Information integriert;
MCQS sollen nun die physikalische Realisierung der sog. komplexen Information sein. Die komplexe Information kann topologisch als spezifisches Muster beschrieben werden, das im Quantennetz realisiert ist. Dieses Quanten-Muster speichert den eingehenden Input durch die Bildung spezifischer Quanten-Produktzustände;
Evtl. erfolgt eine damit implizierte holografische Speicherung in Anlehnung an die Fourier-Transformation, um keine einzelnen „Zahlen“, sondern um „Funktionen“ zu speichern: f(x)=a_0+∑_(n=1)^∞▒(a_n cos〖nπx/L〗+b_n sin〖nπx/L〗 ) ;
Die dynamische Verarbeitung der komplexen Information geschieht dann durch Transformationen der komplexen Information unter Wahrung derselben Komplexitätsklasse, die der komplexe Möglichkeitsraum definiert.
Der komplexe Möglichkeitsraum erfüllt nun folgende Eigenschaften: Er enthält in sich (analog) den Unterraum aller möglichen komplexen Information; er begrenzt den Selektions- und Suchraum der komplexen Information, so dass das System schnell auf den Zielzustand der gesuchten komplexen Information konvergieren kann; er gibt die Regeln bzw. Operatoren der Transformation und Verarbeitung der komplexen Information vor.
Artifiziell erfolgt also die Initiierung eines komplexen Quantensystems, das sich ab dann selbst ordnen und die Aktivierung bzw. Inaktivierung von Quantenpunkten i.S. der quantenmechanischen „Messung“ koordinieren bzw. ordnen soll. Das Hybrid-System aus dem klassischen neuronalen und dem Quantennetz wäre in der Lage, sich an verschiedene visuelle Inputs anzupassen, wobei das (nicht überwachte) Resultat der Anpassung die gesuchte komplexe Information wäre.
Wie könnte der komplexe Möglichkeitsraum definiert werden? Hier kann derzeit nur spekuliert werden. Könnte etwa anstatt eines Basisvektors und seinem Skalar über ein Basis-Fraktal oder Basis-Kristall und seinen analogen Projektionsoperator nachgedacht werden? Dann wäre der komplexe Möglichkeitsraum sowohl „körnig“ bzw. quantisiert als auch begrenzt. In der physikalischen Realität gibt es keine mathematischen Unendlichkeiten, daher bedarf es einer prinzipiellen Begrenzung der Möglichkeiten, komplexe Zustände bzw. eine komplexe Information zu verwirklichen. Ein komplexer Zustand könnte etwa das Tensorprodukt von Basis-Kristallen oder Basis-Fraktalen in dem Raum sein, den sie aufspannen. Die Quantisierung dieses komplexen Möglichkeitsraums erlaubt ferner, die Nichtlinearität der Veränderung einer komplexen Information abzubilden. Ab einem Schwellenwert könnte diese Veränderung als Phasenübergang definiert werden: durch nichtlineare Transformation könnte eine Information von höherer Komplexität und Mächtigkeit und somit eine neue Komplexitätsschicht emergieren. An der mathematischen Beschreibung wird derzeit gearbeitet.
Ordo-Dynamik
Der Definition von Ordnung in Abhebung von Unordnung dient die im Folgenden skizzenhaft vorgeschlagene Ordo-Dynamik. Verschiedene prinzipielle Annahmen fließen in eine noch im Detail auszuarbeitende Theorie der Ordo-Dynamik ein :
Stabilisierung des Quantensystems durch Zunahme der Ordnung (Neg-Entropie) und Abnahme der Wirkung (Minimierung der physikalischen Wirkung). Die physikalische Wirkung wird, so das Postulat, dadurch minimiert, dass sie teilweise in eine informationelle Wirkung transformiert wird . Dabei soll die gesamte Wirkung als Produkt der informationellen und physikalischen Wirkung erhalten bleiben:
W_(ges ) 〖〖= W〗_inf W〗_phys
Bezogen auf Quantensysteme muss ein nicht-klassischer Begriff der (Wechsel-)Wirkung vorausgesetzt werden – bereits Einstein spricht für den Fall von verschränkten Quantenzuständen von einer „Wechselwirkung“ . Eine Quanten-Wirkung jedoch hat einen primär informationellen Charakter, wobei aufgrund des Non-Cloning-Theorems der Begriff der „Information“ keine klassische Information meint, sondern eine Verschränkungs-Information (V-Bit). Ein V-Bit als „besonderer“ Produktzustand von QuBits entspricht einer informationellen Quanten-Wechsel-Wirkung bzw. einer bidirektionalen Relation.
Relationen wiederum ordnen QuBits ähnlich wie die Anordnung von Buchstaben ein sinnvolles Wort ergibt. Insofern V-Bits eine Anordnung bzw. Information unterschiedlicher Komplexität und Ordnung repräsentieren, muss der Raum der erlaubten und möglichen V-Bits durch den komplexen Möglichkeitsraum begrenzt sein.
Ferner wird die makroskopische Relevanz von Quanteneffekten gemäß des Diktums von Erwin Schrödinger postuliert: aus einer Quanten-Ordnung erfolgt makroskopische (raumzeitliche) Ordnung (1944) – und umgekehrt . D.h. ein biologisches System probiert – im Unterschied zu anorganischen Systemen – verschiedene (An-)Ordnungsmöglichkeiten im (begrenzten) komplexen Möglichkeitsraum aus.
Der Begriff der Entropie könnte differenziert definiert werden, um auch bestimmte komplexe Anordnungen als unmöglich auszuschließen. Die thermodynamische Dissipationsskala eines Quantensystems hängt mit der davon unterschiedenen Dekohärenzskala zusammen, was die Ableitung der Entropie aus einem veränderten Enthalpie-Begriff nahelegt, die ihrerseits aus einem anderen Begriff der Wirkung (und Wirklichkeit) von Quantensystemen und –zuständen resultiert.
Diese im Detail zu klärenden Annahmen vorausgeschickt, kann nun der Versuch unternommen werden, ein Postulat der Ordo-Dynamik komplexer Systeme zu formulieren. IE sei die informationelle Energie, H1 die erste Komologie-Gruppe (als mögliche Definition der komplexen Information CI):
IE = E t H^1 ,wobei Energie E und Zeit t reelle Zahlen sind.
Eine Alternative setzt an der Analogie an, die ein universales Prinzip aller Ordnung ist. Die Analogie wird mathematisch ausgedrückt durch die irrationale Zahl φ. Der goldene Schnitt φ wurde in der Philosophie als sog. attributive Analogie ausgedrückt:
A:B = B:C
Ihr könnte eine irrationale Funktion φ (x)= dφ/dx zugeordnet werden. Das legt die Annahme nahe, dass φ die Zahl der Möglichkeiten, Ordnung anzunehmen, begrenzt und daher wesenhaft in die o.g. Definition des komplexen Möglichkeitsraums eingeht. Auch quantenphysikalisch geht bekanntlich φ in einer fundamentalen Weise in die Definition von unitären Operatoren ein. Damit legt sich der Schluss nahe, dass die Wirklichkeit analog strukturiert ist und seine kleinsten Wirkungseinheiten die Signatur der Analogie bzw. Ordnung an sich tragen.
Unabhängig davon lässt sich die informationelle Wirkung in ordo-dynamischen Systemen physikalisch als geordnetes V-Bit auffassen und definieren als:
IE = { ie } ∶= E t CI
Die Neg-Entropie NegS= -S ∶= 1/(k lnW ) kann als Ableitung der komplexen Information verstanden werden, womit die Wahrscheinlichkeit W durch den komplexen Möglichkeitsraum begrenzt wird:
-S= ∂IE∶ ∂ CI
Die Negentropie in komplexen Systemen nimmt dabei nicht ab, sondern ist äquivalent zu: (d CI)/dt ≥0
Die Neg-Enthalpie –H wiederum wird, ohne dabei auf den ontologischen Modus der Wirkung und Wirklichkeit eines Quantensystems einzugehen, definiert als:
-H= ∂IE∶ ∂h
Damit beschreibt die Ordo-Dynamik, dass in der Evolution offene thermodynamische Systeme unter Energieverbrauch zu komplexeren Strukturen und Mustern als Verwirklichungen immer komplexerer Information streben. Dabei lagern sie Entropie an eine „Außenwelt“ ab, was eine Brechung der internen Symmetrie des Systems bedeutet. Parallel dazu nimmt eine „komplexe“ Symmetrie zu, die die komplexe Information CI kennzeichnet:
Einfache Symmetrie S := Komplexe Symmetrie CS
Ein bestimmtes Grad an komplexer Symmetrie definiert topologisch eine Gruppe von periodischen Mustern, d.h. mathematisch ein komplexes Kristall. Dieses wird einer Schicht der komplexen Information bzw. Topologie im Quantensystem zugeordnet. Sie wird definiert durch den komplexen Möglichkeitsraum.
Innerhalb der dadurch definierten möglichen Systemzustände sollen nun diejenigen Zustände selektiert werden, die eine CI koordiniert emergieren lassen. Liegt die CI, wie hier vorgeschlagen, als komplexes Quantensystem vor, so bedeutet eine kontrollierte und künstlich geordnete Emergenz von CI an Quantenpunkten (q dots), dass diese Quantenpunkte räumlich vernetzt und zeitlich geordnet aktiviert werden müssen. Die CI wirkt durch informationelle Energie: die Information löst dann eine Aktivierung oder Inaktivierung eines q dots koordiniert aus. Es werden verschiedene q dots zu Gruppen G (q dots) zusammen gefasst, und diese Gruppen wiederum zu Gruppen G` von größerer informationeller Mächtigkeit als Repräsentationen der jeweiligen Komplexitätsschicht.
Die Zusammenfassung und Ordnung der einlaufenden Information geschieht durch Erfassung der Ordnung der raumzeitlichen Relationen der q dots sowie der Gruppen von q dots, d.h. durch Enkodierung ihrer Relationen i,j:
R(x1,x2)≔〖x12〗_ij für R(x)∈CI
Dadurch bildet sich ein raumzeitliches Muster M. Dieses Muster M ist selbstähnlich und nicht selbst-identisch, weil es sich analog auf verschiedenen Skalen wiederholt bzw. abbildet:
M(n) ∶= vertikale x □(→┴φ ) x´
Das Muster M ist ein Bestandteil des komplexen Möglichkeitsraums R(CI):
M(n) ⊂R(CI)
Bezogen auf die physikalische Wirkungsminimierung gilt: das Produkt aus Wirkung und der Kopplungskonstanten der q dots∶ W_n K_ij ist somit abhängig vom Wirkungsradius r der jeweiligen Ordnungsskala bzw. Komplexitätsschicht. Die Relationen R sind dabei abhängig vom goldenen Schnitt φ (=topologische Definition auf Basis der sog. analogen Projektion).
Um nun die Dynamik der Ordnung zu erfassen, kann die Veränderung des Musters M in Abhängigkeit von Ort und Zeit begriffen werden:
M(n)dynamisch∶= (∂ M (n))/(∂t ∂(x,y,z))
Die Emergenz von holistischer Ordnung
Wie entsteht nun konkrete Ordnung in lebendigen Systemen statt eines Chaos? – Durch den o.g. „zentralen Ordner“ bzw. durch den komplexen Möglichkeitsraum. Er trennt gewissermaßen die Ordnung vom Chaos, indem es die Anzahl der Möglichkeiten der Emergenz bzw. der Selbst-Ordnung begrenzt. Die Dynamik der komplexen Informationsverarbeitung geschieht in diesem komplexen Möglichkeitsraum. Ohne eine solche Vorgabe eines komplexen Möglichkeitsraums (in Entsprechung zu den eingangs genannten Schemata) wäre eine geordnete Selbstorganisation nicht möglich.
Warum bedarf es überhaupt einer komplexen Ordnung in einem Quantensystem? Weil der komplexen Information ein mehrschichtiges System entsprechen soll (sog. Schichtenmodell) und weil so die entscheidenden Vorteile der Quanteninformationsverarbeitung (Geschwindigkeit, Energie-Effizienz, ultraschnelle Parallelverarbeitung, physikalische Realisierung komplexer Information) genutzt werden können. Ohne ein mehrschichtiges komplexes Quantensystem als analoges Korrelat eines neuronalen Netzwerks ist es schwer vorstellbar, wie die komplexe Informationsverarbeitung physikalisch implementiert werden kann.
Anhand eines Präparationsvorgangs von QuBits und V-Bits an künstlich platzierten Quantenpunkten sollte daher ein mehrschichtiges komplexes Quantensystem entstehen. Die komplexen (fraktalen?!) Aktivierungsmuster, die zur Initiierung des hybriden neuronalen Netzes führen, könnten durch eine Vorschrift erzeugt werden, die der folgenden fraktalen Funktion genügt:
f(x)=x^2+ C ,wobei x/(x`)= f (φ)
Das hybride System soll etwa beim autonomen Autofahren einer spezifischen Mustererkennung dienen, indem sie die beiden Komplexitätsschichten im Quantensystem emergieren lässt. D.h. das System bildet die physikalische Implementierung des spezifischen komplexen Möglichkeitsraums ab, der die Summe der Verkehrsschilder in Form von komplexer Informationen definiert. Während des Zuordnungsprozesses wird eine komplexe Information CI(n) auf CI(n+1) gemappt bzw. durch Anwendung eines komplexen Operators ineinander transformiert. Welcher Operator angewandt wird, soll Resultat eines Selbstorganisationsprozesses sein und ist nicht durch den komplexen Möglichkeitsraum determiniert.
Wie erwähnt, bildet auch das Quantensystem ein mehrschichtiges Quanten-Netz. Die Verbindungen zwischen QuBits wären die V-Bits. Welche Kombination bzw. Anordnung von V-Bits ist nun erlaubt? Hier ist es hilfreich, auf den Prozess der Selbstassemblierung zu schauen. Das System organisiert sich selbst in Richtung der gewünschten komplexen Information als Output. Dieser Prozess kann als Bewegung im Raum der möglichen (An-)Ordnungen der QuBits bzw. als Veränderung der Quanten-Topologie bis zur gewünschten Topologie modelliert werden. Dann gilt für die Wahrscheinlichkeit der Bewegung des Systemzustands Z in Richtung der gesuchten komplexen Information CI:
W für Z(t0)→Z(t1): Z(t1)=Z(t0) lnW(CI)
Man beachte: der Prozess der Selbstorganisation ist historisch relevant, d.h. das System besitzt im Unterschied zu einem Markov-Prozess eine historische Spur bzw. ein Gedächtnis, so dass die vergangenen Korrelationen in die zukünftige Entwicklung des Systems konstitutiv mit eingehen.
Durch Synergien soll es nun zur „antriebsabhängigen“ zeitlichen (Synchronizität) und räumlichen (Ensemblebildung) Koordination kommen. Die Synergien, die zu einer CI passen, setzen entsprechende Kopplungsstärken KS voraus. Sie sollte proportional zum Kehrwert der Entropie S mal einer Komplexitätskonstante C sein: KS (q1,q2)=1/S C
Die Bewegung des Systems approximiert nun den Zustand des Gesamtsystems mit maximaler CI, so dass gilt:
KS gesamt= ∫_q1^qn▒〖KS ∂CI〗
Somit gibt es lediglich eine allgemeine Selektionsregel für das Zustandekommen der gewünschten Synergien, dass CI zunimmt und die Wirkung W in Abhängigkeit von der Komplexitätskonstante C abnimmt:
CI=1/W C
Der Selektionsdruck wird also durch das Prinzip der Minimierung der Wirkung vorgegeben und bestimmt die Wahl des jeweiligen Transformationsoperators. Physikalisch wird ein Teil der Wirkung, die generell als Ansammlung von Information beschrieben werden kann, in komplexe Information zurück-transformiert. Daraus folgt die Abnahme und Auslagerung der Entropie durch Zunahme der Komplexität. Das wiederum führt zur sukzessiven Realisierung immer komplexerer Information.
Definition und Verarbeitung der dynamischen komplexen Information
Der komplexe Möglichkeitsraum bestimmt also die endliche Anzahl der topologischen komplexen Information. Sie hat folgende Eigenschaften:
Die komplexe Information kann als komplexe (geometrische und algebraische) Topologie verstanden werden
Die komplexe Information ist holistisch und nichtlokal
Die komplexe Information ist höher-dimensional und ist eine Untermenge des komplexen Möglichkeitsraums
Die komplexe Information kodiert die Relationen (zwischen Bits, aber auch zwischen QuBits) und definiert bzw. begrenzt somit die Menge möglicher Muster.
Die komplexe Information des R^3 kann nun nach Peter Nonnemann anhand der sog. Garben-Kohomologie definiert werden ( H^n ∶n∈N ). Zusammen mit Peter Nonnenmann behaupte ich, dass herkömmliche Bilderkennungssysteme, z. B. Deep-Learning-Netze in selbst-fahrenden Autos, holistische Figuren, Muster und Topologien nicht „erkennen“, d.h. semantisch verstehen können, da Deep-Learning-Netze nur lokal einzelne Pixel verarbeiten. Nonnenmann definiert die komplexe Information des R^3 folgendermaßen :
KI ( R^3 ) ∶= H^1 ( Q ,R^+ )
Resümee
Die Untersuchung der höheren Kohomologie-Gruppen H^2,H^3,… auf ihre Nützlichkeit für noch komplexere KI-Probleme soll weiterbetrieben werden. Die künftige KI wird nicht um die Implementierung der komplexen Information und –verarbeitung umhin kommen. Schließlich wird dadurch die holistische Identifikation von Perzepten ebenso ermöglicht wie die Zuordnung bzw. Gruppierung von Inputs auch ohne einen immensen Trainingsaufwand mit einer möglichst großen Datenmenge. Die komplexe Informationsverarbeitung bezieht sich auf den Prozess der (Re-)Konstruktion der gesuchten komplexen Information.
Der Prozess der Rekonstruktion meint im Einzelnen:
Assoziation der einlaufenden Information mit vorhandener Information: Verbindung und Trennung möglicher Relationen zwischen den Informationseinheiten, die ihrerseits in neuronalen Gruppen bzw. „Modulen“ auf einer gegenüber dem einzelnen Neuron höheren (emergenten) Skala repräsentiert sind.
Kombination von Informationseinheiten zu emergenten Gruppen, wobei passende Kombinationen positiv selektiert werden. Die Selektion erfolgt also auf der Ebene von komplexen Informationseinheiten bzw. neuronalen Gruppen.
Der komplexe Möglichkeitsraum gibt dabei die Regeln der Verbindung und Trennung von Relationen an bzw. definiert die möglichen Operatoren, ohne Ihre Aktivierung im einzelnen zu determinieren.
Zur komplexen Informationsverarbeitung stellt sich technologisch u.a. die Frage, welche klassische (An-)Ordnung von q dots zur Emergenz der gesuchten komplexen Information überhaupt geeignet ist. Sobald das erste reverse Feedback erfolgreich gestartet wurde, ordnet sich das System fortan selbst (geordnete Selbstorganisation) wie das biologische neuronale Netz und erzeugt die gewünschten Outputs. Die quantenbasierte topologische komplexe Informationsverarbeitung könnte das physikalische Substrat einer komplexen Informationsverarbeitung darstellen.
Die komplexe Information ist eine holistische und integrative Information, die einerseits das Ergebnis eines Generalisierungsprozesses durch Emergenz ist, andererseits durch vorgegebene Schemata bzw. durch den komplexen Möglichkeitsraum überhaupt erst definiert ist und zustande kommt. So wird im Rahmen einer vorgegeben komplexen Ordnung des komplexen Möglichkeitsraums eine eigene Ordnung kreativ erzeugt! Diese emergente Ordnung ist Resultat von künstlich induzierten Selbstorganisationsprozessen und repräsentiert hochgradig komplexe adaptive Reaktionen und autonom-flexible Aktionen in Echtzeit – ein Meilenstein auf dem Weg zur ersten „echten“ Künstlichen Intelligenz!


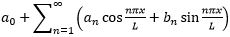
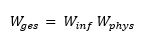
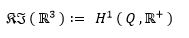

Um einen Kommentar zu hinterlassen müssen sie Autor sein, oder mit Ihrem LinkedIn Account eingeloggt sein.