Der vorliegende Beitrag beschreibt ein Vorgehen zur Berechnung von Preissensitivitätskurven als Grundlage des Revenue Managements zur Vergabe von Transportauftragen durch eine Spedition. Das Vorgehen ist Teil eines durch den mFUND (Forschungsinitiative des Bundesministeriums für Verkehr und digitale Infrastruktur) geförderten Projektes zur Entwicklung einer vollumfänglichen digitalen Spedition in Deutschland.
Hintergrund
Modernes Pricing bedeutet heute nicht mehr, einen Preis für ein Produkt bzw. eine Dienstleistung in Abhängigkeit der Kosten zu erheben, sondern vielmehr, den maximalen Preis zu finden, welcher ein Kunde bereit ist, zu zahlen. Die Kaufbereitschaft bzw. die Kaufwahrscheinlichkeit ist dabei kundenspezifisch und hängt neben dem Preis von unterschiedlichen Einflüssen ab. Beispielsweise sind für einen Businessreisenden eine kurzfristige Buchungsmöglichkeit und die Flexibilität des Abflugs bzw. der Abfahrt oftmals wichtiger als ein geringer Ticketpreis. Auch kann sich die Kaufwahrscheinlichkeit eines Kunden ändern, wenn sich beispielsweise die Wettervorhersage ändert.
Der funktionale Zusammenhang zwischen dem Preis und der Kaufwahrscheinlichkeit unter Berücksichtigung aller weiterer Einflüsse wird als Preissensitivität bezeichnet. Variiert man den Preis für das Produkt bzw. die Dienstleistung, erhält man aus der Preissensitivität eine Kurve in Abhängigkeit des Preises. Zur Berechnung solcher Kurven wird im Folgenden ein Verfahren des maschinellen Lernens vorgestellt.
Problemstellung
Eine Spedition in Deutschland vermittelt Transportaufträge zwischen einem Versender und einem Transportunternehmen. Bei den Speditionen übernehmen diese Aufgabe heute Disponenten, welche die Preise für den Versender und die Preise für das Transportunternehmen i.A. telefonisch anbieten und nachverhandeln. Die Differenz zwischen den Einnahmen durch den Versender und den Ausgaben an das Transportunternehmen ergibt die Marge für die Spedition.
Zur digitalen Transformation des Angebotsprozesses für das Transportunternehmen wird die telefonische Preisverhandlung zwischen dem Disponenten und dem Transportunternehmen durch einen nichtverhandelbaren Fixpreis ersetzt. Die Berechnung dieses Preises wird durch ein Verfahren des maschinellen Lernens übernommen, welches nicht nur tour- und sendungsspezifische Parameter berücksichtigt, sondern auch Eigenschaften des Transportunternehmens wie beispielsweise die regionale Erfahrung im Bereich des Transportes. Hinzu kommen weitere externe Einflüsse wie eine Preissaisonalität und zeitlich nahe Feiertage.
In der digitalen Spedition erfolgt das Vorgehen zur Vergabe von spezifischen Aufträgen an geeignete Transportunternehmen in zwei aufeinander aufbauenden Modulen. Im ersten Schritt wird auf Basis historischer Angebotsinformationen für jedes bekannte Transportunternehmen eine individuelle Preissensitivitätskurve bestimmt, was Inhalt des vorliegenden Beitrags ist. Die resultierenden Kurven werden im Anschluss an eine künstliche Intelligenz übergeben, welche die Kurven analysiert, die geeignetsten Transportunternehmen selektiert und für diese Unternehmen die Angebotspreise so bestimmt, dass diese den Auftrag mit einer hohen Wahrscheinlichkeit annehmen. Dabei darf die Marge der Spedition nicht aus den Augen verloren werden. Weiter muss die Fristigkeit eines Transportes berücksichtigt werden: bei einem langen Vorlauf können die Preise niedriger angesetzt werden, um ggf. eine höhere Marge zu erreichen. Für Transporte mit kurzen Vorlaufzeiten müssen hohe Annahmewahrscheinlichkeiten gelten.
Ziel
Die Frage, ob ein Unternehmen einen angebotenen Transportauftrag annimmt, hängt zu einem großen Teil vom angebotenen Preis ab: je höher der Preis desto eher wird das Unternehmen den Transport durchführen. Wie eine Studie der Universität St. Gallen zeigt (vgl. [St. Gallen 2019]), haben aber auch andere Parameter Einfluss auf die Annahme eines Transportauftrages. Führt beispielsweise der Transport in eine wirtschaftlich schwache Region mit wenigen potentiellen Versendern, ist es schwer, den Transporter für den Rückweg gut auszulasten. Dies führt zu geringeren Annahmewahrscheinlichkeiten für solche Touren.
Das Ziel des Vorgehens ist eine Schätzung der unternehmensspezifischen Annahmewahrscheinlichkeit für einen spezifischen Transport in Abhängigkeit eines gegebenen Preises unter Berücksichtigung aller vorhandenen Informationen. Diese Abhängigkeit lässt sich durch Variation des Preises zu den benötigten Preissensitivitätskurven verdichten, welche wiederum als Basis zur Bestimmung eines Preises dient, zu dem das individuelle Unternehmen den Transport mit einer erwarteten Wahrscheinlichkeit übernehmen wird.
Algorithmus
Der Algorithmus soll einen funktionalen Zusammenhang zwischen den unterschiedlichen Einflussmerkmalen inkl. des Transportpreises und der Annahmewahrscheinlichkeit als Zielgröße für einen spezifischen Transport herstellen. Da die Annahmewahrscheinlichkeit unbekannt ist, wird stattdessen das binäre Merkmal Auftragsannahme herangezogen und die Wahrscheinlichkeit der Zusage durch ein Transportunternehmen als Annahmewahrscheinlichkeit interpretiert.
Bei der Auswahl eines Algorithmus‘ muss berücksichtigt werden, dass der Merkmalraum sehr hoch dimensioniert ist, wodurch klassische mathematische und statistische Verfahren ausgeschlossen werden müssen. In der aktuellen Problemstellung werden 18 Merkmale berücksichtigt, welche im Abschnitt Merkmale beschrieben werden. Neben Verfahren der mehrdimensionalen Regression (vgl. exemplarisch [Windzio 2013]) oder der gauß’schen Prozesse (vgl. exemplarisch [Mishura 2018]) nutzt man für ähnliche Problemstellungen üblicherweise ein trainiertes künstliches neuronales Netz (vgl. exemplarisch [Rojas 1996]), bei dem die Anzahl der Merkmale und die Anzahl der Zielgrößen sehr groß sein kann. Ein weiterer Vorteil von künstlichen neuronalen Netzen ist die Berücksichtigung von Abhängikeiten der Merkmale untereinander.
Zur Bestimmung der Annahmewahrscheinlichkeiten wird zusätzlich ein Monotoniekriterium für einzelne Merkmale vorausgesetzt. So wird beispielsweise eine monoton wachsende Annahmewahrscheinlichkeit bei einer Erhöhung des Preises gefordert.
In [Mahul 2004] werden Anpassungen von künstlichen neuronalen Netzen zur Umsetzung von Monotoniebedingungen vorgeschlagen. Die Ansätze besitzen allerdings eine hohe Komplexität und wurden bisher nicht ausreichend für praktische Anwendungen untersucht.
Zur Herstellung des funktionalen Zusammenhangs zwischen den Merkmalen und der Zielgröße wurde in dieser Arbeit ein Deep Lattice Netzwerk (DLN; vgl. [You 2017]) trainiert, welches die oben genannten Anforderungen erfüllt. Das Verfahren besteht im Kern aus einem n-dimensionalen Hyperwürfel der Kantenlänge 1, wobei n die Anzahl der Merkmale beschreibt. Es wird also durch jede Dimension des Würfels ein Merkmal abgebildet. In den Würfel legt man eine (mehrdimensionale) Funktion, welche den Zusammenhang zwischen den Merkmalen und der Zielgröße abbildet. Dazu werden für die Eckpunkte des Würfels, welche die variablen Parameter des Modells darstellen, Funktionswerte auf Basis von Trainingsdaten berechnet. Zwischen den Eckpunkten wird die Zielfunktion linear interpoliert. Zur Erhöhung der Detaillierung der Funktion können die Kanten des Würfels unterteilt werden. Durch die Teilungspunkte wird ein Gitter (Lattice) gelegt, dessen Schnittpunkte als zusätzliche Parameter des Modells mit Funktionswerten belegt werden.
In der folgenden Abbildung ist ein Lattice mit zwei Merkmalen (also ein Quadrat) dargestellt. Für die vier Eckpunkte θ[i] als Parameter des Modells wurden Werte aus einer Menge aus Trainingsdaten abgeleitet. Die darzustellende Funktion f(x) wurde durch lineare Interpolation zwischen den Eckpunkten erreicht. Weitere Stützstellen zwischen den Eckpunkten zur Verdichtung des Gitters und zur Erhöhung des Detailierungsgrades der Funktion wurden nicht verwendet.
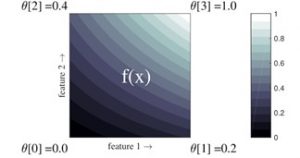
Zur Bestimmung der Annahmewahrscheinlichkeiten wird als Verlustfunktion des Trainings die sogenannte Kreuzentropie verwendet (vgl. [Murphy 2012]). Durch Variation des Preises unter Fixierung der weiteren Merkmale erhält man aus dem Deep Lattice Netzwerk die gesuchte Preissensitivitätskurve.
Daten
Für ein Verfahren des maschinellen Lernens werden Trainingsdaten benötigt. Die historischen Transportdaten wurden von einer großen deutschen Spedition mit mehreren Standorten in und außerhalb von Deutschland bereitgestellt. Die Daten wurden umfangreich bereinigt, um den Einfluss von Datenfehlern auf das Trainingsergebnis zu minimieren. Eine Zeile in den strukturierten Daten enthält jeweils die Informationen zu dem Transport einer Sendung inkl. des binären Merkmals Annahme des Angebotes durch das Transportunternehmen. Um die Auslastung von LKW zu erhöhen und damit die Transportkosten zu reduzieren, wird versucht, mehrere Sendungen zu einem Transport zusammenzufassen. Diese Information wird in den Daten durch eine gemeinsame Transport-ID gekennzeichnet. Die Merkmale von zusammen transportierten Sendungen werden zu Transportdatensätzen aggregiert.
Im Folgenden werden Annahmen notwendig sein, um bisher nicht gemessene Einflüsse eines Transportes im Modell berücksichtigen zu können. Unsichere Annahmen können zu großen Abweichungen im Ergebnis des Algorithmus‘ führen und damit zu Fehlentscheidungen, welche z.B. zu Umsatzverlusten führen können. Unternehmen sollten frühzeitig Prozesse zur Messung der fehlenden Werte einführen, um die notwendigen Annahmen mit tatsächlich gemessenen Werten kontrollieren bzw. beim Vorliegen einer ausreichend großen Datenmenge sie schrittweise ersetzen zu können.
Merkmale
In der aktuellen Version des Modells werden 18 Merkmale zur Erklärung der binären Zielgröße Auftragsannahme berücksichtigt. Diese sind im Folgenden beschrieben.
- tatsächlich gezahlter Transportpreis in Euro
Bei mehreren Sendungen, welche zu einem Transport zusammengefasst wurden, werden die Transportpreise der einzelnen Sendungen summiert.
- Distanz in Kilometer
In den zur Verfügung gestellten Daten liegt für jede Sendung die optimale Distanz aus einem Online-Routenplaner vor. Bei mehreren Sendungen, welche zu einem Transport zusammengefasst wurden, wird zur Vereinfachung die maximale Distanz zwischen der Be- und der Entladestelle einer Sendung verwendet. Die tatsächliche Distanz lag in den Daten nicht vor.
- Lademeter
Ein Lademeter ist ein typisches Maß zur Beschreibung der benötigten Ladefläche für eine Sendung auf einem Transporter. Er entspricht dabei einem Rechteck mit einer Länge von einem Meter in Fahrtrichtung und einer Breite entsprechend der Transporterbreite.
Bei mehreren Sendungen, welche zu einem Transport zusammengefasst wurden, werden die Lademeter summiert.
- Gewicht in Tonnen
Bei mehreren Sendungen, welche zu einem Transport zusammengefasst wurden, werden die Einzelgewichte summiert.
- Geokoordinaten (4 Merkmale)
Die Geokoordinaten bestehen aus der Longitude und der Latitude für die Beladestelle und für die Entladestelle. Bei mehreren Sendungen, welche zu einem Transport zusammengefasst werden, werden unter der Annahme, dass die Ladestellen in räumlicher Nähe zueinander liegen, die Geokoordinaten gemittelt.
- Wochentag
Entspricht dem Wochentag der Abfahrt des Transportes bzw. dem Wochentag der Abfahrt bei der ersten Beladestelle.
- Arbeitstage
Entspricht der Anzahl der Arbeitstage in der Woche der Abfahrt des Transportes bzw. in der Woche der Abfahrt bei der ersten Beladestelle. Hierbei wurden Feiertage berücksichtigt, welche in mindestens fünf deutschen Bundesländern existieren. Brückentage zwischen Feiertagen und Wochenenden bzw. zwischen Feiertagen wurden mit einem Abzug von 0,5 Tagen berücksichtigt.
- Feiertag
Liegt ein Feiertag näher als fünf Tage am Abfahrttag des Transportes bzw. am Abfahrttag der ersten Sendung, wir die binäre Variable mit 1 belegt. Hierbei wurden Feiertage berücksichtigt, welche in mindestens fünf deutschen Bundesländern existieren.
- Monat
Entspricht dem Monat der Abfahrt des Transportes bzw. dem Monat der Abfahrt bei der ersten Beladestelle.
- Jahr
Entspricht dem Jahr der Abfahrt des Transportes bzw. dem Jahr der Abfahrt bei der ersten Beladestelle.
- Fahrdauer in Stunden
Für LKW-Fahrer gelten in Deutschland gesetzliche vorgeschriebene Ruhezeiten. Besonders darf ein LKW-Fahrer pro Tag nicht länger als neun Stunden sein Fahrzeug lenken (vgl. [EU 2006]). Dauert ein Transport länger, muss der Fahrer den restlichen Tag pausieren. Um diese Pausenzeiten, aber auch weitere zeitliche Verzögerungen wie Wartezeiten oder Be- und Entladezeiten im Modell zu berücksichtigen wurde ein künstliches Merkmal Fahrdauer erzeugt.
Ein guter Startpunkt für die Bestimmung der Einflüsse findet man beispielsweise in [Vogel 2020].
- Hin- / Rücktour
Wie bereits beschrieben, erhöht sich die Annahmewahrscheinlichkeit für einen Transport, wenn die Tour in die Nähe der Niederlassung des Transportunternehmens führt. Um dies zu berücksichtigen, wurde aus den historischen Daten für alle Transportunternehmen Geokoordinaten für Niederlassungen durch Clusterung von ähnlich gelegenen Be- und Entladestationen geschätzt. Aus diesen Informationen wurde für jeden historischen Transportauftrag bestimmt, ob sich der Transport von einer Niederlassung entfernt oder sich ihr nähert.
- Entfernung zu Niederlassung in Kilometer
Gibt die minimale Entfernung als Fluglinie in Kilometer von einer Niederlassung des Transportunternehmens zu einer Be- oder Entladestelle an.
- typischer Fahrbereich in Kilometer
Neben der Schätzung von Geokoordinaten für Niederlassungen eines Transportunternehmens wurden typische Regionen der Transporte, ausgehend von den Niederlassungen, geschätzt. Zur Vereinfachung wurden die Regionen durch Geokoordinaten der linken unteren Ecke und der rechten oberen Ecke eines Rechtecks beschrieben. Das Merkmal gibt an, wie weit die von der Niederlassung maximal entfernteste Be- oder Entladestation innerhalb oder außerhalb des Rechtecks liegt. Die Entfernung wird als Luftlinie senkrecht zur nähesten Kante des Rechtecks in Kilometer angegeben.
Der Wert von Daten bzw. von Informationen darf nicht unterschätzt werden. Die genutzten Merkmale basieren teilweise auf unsicheren Annahmen, welche zu fehlerhaften Modellausgaben führen können. Die Geokoordinaten von Niederlassungen der Transportunternehmen oder deren typische Anfahrtsbereiche sind Informationen, welche bei den Transportunternehmen vorliegen und der Spedition zur Verfügung gestellt werden könnten. Damit könnte die Spedition den Transportunternehmen geeignetere Aufträge oder durch eine Steigerung der Sicherheit bei der Berechnung der Preis-Annahme-Abhängigkeiten höhere Transportpreise anbieten. Weitere Informationen wie beispielsweise die Größe und die Zusammensetzung des Fuhrparks können zu einer häufigeren Berücksichtigung des Transportunternehmens bei der Vergabe von Aufträgen führen. Auch die Begründung eines abgelehnten Angebotes oder eine nachträgliche Bewertung eines durchgeführten Transportes sind wichtige Informationen für eine digitale Spedition. Wichtig ist die Einsicht, dass Informationen einen Wert haben und die Weitergabe zu einem Mehrwert für das Transportunternehmen führen muss.
Realisierung
Die stetigen Merkmale liegen in unterschiedlichen Wertebereichen vor. Beispielsweise ist die maximale Kapazität eines LKW 13,6 Lademeter und der Transportpreis liegt im Intervall zwischen 200€ und 1.500€ vor. Für grundsätzlich gleiche Einflüsse der Merkmale wurden diese durch den sogenannten Min-Max-Scaler (vgl. [Loukas 2020]) in das Intervall [0, 1] skaliert. Die nicht-metrischen Merkmale wie der Wochentag oder die Unterscheidung zwischen Hin- und Rücktour wurden für den Algorithmus als nominale Merkmale definiert und beim Training entsprechend als solche berücksichtigt.
Die Annahmewahrscheinlichkeit wird auf Basis der oben beschriebenen 18 Merkmalen unter Verwendung eines Deep Lattice Netzwerkes geschätzt. Der Parameterraum wird neben den zwei Eckpunkten pro Merkmal durch 18 zusätzliche Stützstellen pro Merkmale aufgespannt. Dadurch wird jede Kante in 19 gleichgroße Segmente geteilt, wodurch ein Würfel bzw. ein Modell zur Abbildung des Zusammenhanges zwischen den Merkmalen und der Auftragsannahme eines Transportauftrages mit 2018 = 260 Trilliarden zu optimierender Parameter entsteht.
Zur Reduzierung der Komplexität wurden die Merkmale in sechs Dreiergruppen aufgeteilt, für die jeweils separate Modelle mit der Zielgröße Auftragsannahme trainiert werden. Die Ergebnisse der einzelnen Modelle werden nach dem Abschluss aller Trainings zusammengeführt. Die Zuordnung der Merkmale zu den Gruppen erfolgt auf Basis der Ähnlichkeiten der Merkmale durch den sogenannten Crystals-Algorithmus (vgl. [Fard 2016]). Damit erhält man sechs dreidimensionale Würfel mit jeweils 20³ = 8.000 Parameter, also insgesamt 48.000 Parameter. Die Ergebnisse werden anschließend in Form von gemittelten Kurven zusammengeführt. Zur Festlegung der Zuordnung von Merkmalen zu einem Würfel sowie zum eigentlichen Training der Parameter wurde der Adam-Algorithmus (Adaptive Moment Estimation-Algorithmus; vgl. [Kingma 2014]) mit einer festen Lernrate bzw. Schrittweite verwendet.

Ergebnisse
Aufgrund des großen Merkmalsraum ist es nicht möglich, alle Kombinationen zu analysieren. Mit beispielsweise durchschnittlich fünf Ausprägungen pro Merkmal ergeben sich 185 = 1,9 Millionen Merkmalkombinationen. Aus diesem Grund erfolgt die Analyse der Ergebnisse qualitativ durch die Definition eines Standardtransportes, für den alle Merkmale separat variiert werden. Es ist dabei zu beachten, dass die dargestellten Einflüsse nur für den definierten Standardtransport gelten und keinen Anspruch auf Allgemeingültigkeit haben. Die Fahrdauer als künstliches Merkmal wird nicht explizit dargestellt, da sie sich aus den Merkmalen Sendungsanzahl, maximale Distanz und Lademeter ergibt. Die Anzahl der Ausprägungen wird merkmalspezifisch festgelegt. Die Ausprägung des Standardtransportes ist in jeder Abbildung als grüne Kurve dargestellt.
Einfluss der Geokoordinaten
Der Standardtransport erfolgt aus einer wirtschaftlich starken Region in Deutschland (man spricht von einem Hotspot im Unterschied zu einer wirtschaftlich schwachen Region, welche als Coldspot bezeichnet wird) in eine ebenfalls wirtschaftlich starke Region mit einer Distanz von etwa 400 Kilometer. Zur Validierung des Einflusses unterschiedlicher Regionen werden drei weitere Transporte mit gleichen Merkmalen definiert
- aus einer wirtschaftlich starken Region in eine wirtschaftlich schwache Region mit einer Distanz von etwa 400 Kilometer
- aus einer wirtschaftlich schwachen Region in eine wirtschaftlich schwache Region mit einer Distanz von etwa 400 Kilometer
- aus einer wirtschaftlich schwachen Region in eine wirtschaftlich starke Region mit einer Distanz von etwa 400 Kilometer
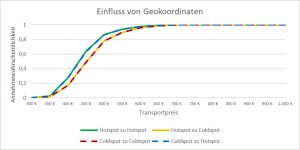
Man erkennt, dass Transporte in einen Coldspot teurer sind, als Transporte in einen Hotspot, bzw. die Preissensitivitätskurven eine flachere Steigung haben. Der Grund dafür ist das Risiko, den LKW auf der Rücktour nur gering ausgelastet zu bekommen bzw. sogar vollständig leer zurückzufahren. Die wirtschaftliche Lage der Abfahrregion hat keinen oder nur einen geringen Einfluss auf den Transportpreis.
Einfluss Sendungsanzahl
Der Standardtransport umfasst eine Sendung (man spricht von einem Full-Truck-Load bzw. FTL). Zur Validierung wurden Transporte mit 2 und 3 Sendungen definiert (man spricht von einem Less-Than-Full-Truck-Load bzw. LTL). Die Auslastung und die Distanz wurde durch die Erhöhung der Sendungsanzahl nicht verändert.
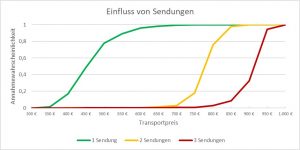
Man erkennt, dass die Anzahl der Sendungen einen großen Einfluss auf die Annahmewahrscheinlichkeit bzw. den Preis hat. Die Gründe dafür sind zusätzliche Fahrkilometer, Wartezeiten und Ladezeiten. Der Unterschied zwischen einer und zwei Sendungen ist größer als der zwischen zwei und drei Sendungen.
Einfluss der Lademeter
Der Standardtransport umfasst 9 Lademeter. Zur Validierung des Einflusses wurden Transporte mit 4 und 13,6 Lademeter definiert (Hinweis: 13,6 Lademeter entsprechen der Ladefläche eines typischen LKW mit Anhänger bzw. eines Sattelschleppers).
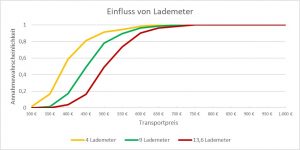
Man erkennt, dass mit einer Zunahme der Lademeter auch der Transportpreis steigt. Der Grund dafür ist die Zunahme der Be- und Entladezeiten durch weitere Ladegüter.
Einfluss des Gewichtes
Der Standardtransport umfasst 15 Tonnen Ladungsgewicht. Zur Validierung des Einflusses wurden Transporte mit 5 und 24 Tonnen Ladungsgewicht definiert (Hinweis: 24 Tonnen Ladungsgewicht entsprechen der zulässigen Zuladung eines typischen LKW mit Anhänger bzw. eines Sattelschleppers).
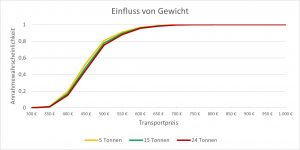
Man erkennt, dass das Ladungsgewicht keinen signifikanten Einfluss auf den Transportpreis hat. Die zu sehenden Unterschiede resultieren wahrscheinlich aus dem höheren Dieselverbrauch durch die größere Masse.
Einfluss des Monats
Der Standardtransport wurde in einem Juni durchgeführt. Zur Validierung wurden identische Transporte im Februar, April, August, Oktober und Dezember definiert.
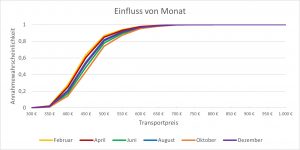
Man erkennt, dass der Februar und der April die günstigsten Monate für einen Transport sind, der Oktober der teuerste. Im Dezember ist der Transportpreis durchschnittlich hoch.
Einfluss des Jahres
Der Standardtransport wurde im Jahr 2021 durchgeführt. Zur Validierung wurden identische Transporte in den Jahren 2019 und 2020 definiert.
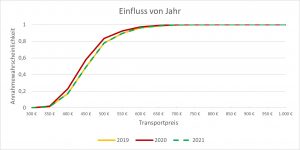
Man erkennt, dass die Jahre 2019 und 2021 ähnliche Transportpreise haben. Ob die zu erkennenden Abweichungen für das Jahr 2020 aus der Corona-Pandemie resultieren, müsste näher untersucht werden.
Einfluss der Arbeitstage
Der Standardtransport wurde in einer Woche mit fünf Arbeitstagen durchgeführt. Zur Validierung wurden identische Transporte in Wochen mit einem, zwei, drei und vier Arbeitstagen definiert.
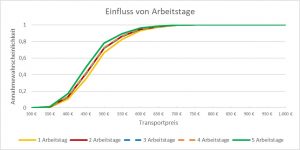
Man erkennt, dass mit Reduzierung der Arbeitstage in einer Woche der Transportpreis steigt. Bei der Darstellung ist zu beachten, dass es wenige Wochen in den historischen Daten gab, welche nur einen oder zwei Arbeitstage hatten.
Einfluss von Hintour und Rücktour
Der Standardtransport wurde als Rücktour definiert (die Entladestelle liegt also näher an der Niederlassung des Transportunternehmens als die Beladestelle). Zur Validierung wurde ein identischer Transport als Hintour definiert.
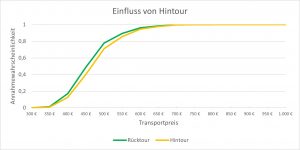
Man erkennt, dass die Rücktour günstiger ist, als die Hintour. Grund dafür ist der Wegfall des Risikos, dass der anschließende Transport mit einer geringen Auslastung oder sogar leer gefahren werden muss. Zudem kann der Fahrer ggf. zuhause übernachten.
Einfluss des typischen Fahrbereiches
Der Standardtransporte führte exakt an die Grenzen des typischen Aktionsbereiches des Transportunternehmens in den historischen Daten. Zur Validierung wurden identische Transporte mit Zielen definiert, welche 300 Kilometer bzw. 150 Kilometer innerhalb der Grenzen und 150 bzw. 300 Kilometer außerhalb der Grenzen lagen.
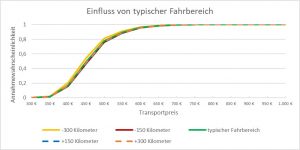
Man erkennt, dass Transporte mit einem großen Abstand zu den Grenzen innerhalb des typischen Aktionsbereiches des Transportunternehmens zu einer Reduzierung des Transportpreises führen. Be- oder Entladestellen außerhalb des Bereiches haben keinen oder nur einen sehr geringen Einfluss.
In den Diagrammen zu den Einflüssen des Wochentages, eines Feiertages und der Entfernung zur Niederlassung konnten keine signifikanten Unterschiede erkannt werden. Aus diesem Grund wurden sie hier nicht dargestellt.
Noch einmal der Hinweis, dass sich alle dargestellten Einflüsse nur auf den gewählten Transport beziehen und keine allgemeingültige Interpretation zulassen. Beispielsweise kann der Einfluss des Wochentages in einer anderen Region einen abweichenden Einfluss haben oder auch in einem anderen Monat, in einem anderen Jahr oder wenn mehr als eine Sendung transportiert werden soll.
Fazit und weiteres Vorgehen
Man sieht, dass die Anforderungen an den Algorithmus erfüllt wurden und ein Verfahren gewählt wurde, mit dem man aus historischen Transportaufträgen einer Spedition unternehmensspezifische Preissensitivitätskurven zur Abbildung des funktionalen Zusammenhanges des Transportpreises und der Annahmewahrscheinlichkeit berechnen kann.
Die Berechnung erfolgt auf Basis von 18 Merkmalen, welche teilweise auf Annahmen beruhen. Für diese Merkmale sollte ein Prozess zur Messung bzw. Beschaffung der tatsächlichen Werte etabliert werden. Ein weiterer Punkt in diesem Zusammenhang ist die Verwendung von Durchschnittswerten für die angenommenen Größen. Beispielsweise liegt eine andere Durchschnittsgeschwindigkeit auf Landstraßen vor als auf Autobahnen und 100 Kilometer im Ruhrgebiet dauern ggf. länger als 100 Kilometer in einer weniger besiedelten Gegend und zusätzlich ist die Fahrdauer abhängig von der Uhrzeit der Fahrt. Zur Verbesserung der Modellgüte sollten die Annahmen auftragsspezifisch festgelegt werden.
Eine weitere Möglichkeit zur Verbesserung der Prognosequalität ist die Einbeziehung von aktuellen externen Informationen wie die Verkehrs- oder die Wettersituation auf der Tour. Auch besondere Veranstaltungen wie Messen führen zu einer Erhöhung der Transportpreise und entsprechend zu geringeren Annahmewahrscheinlichkeiten bei konstanten Preisen. Ebenso lässt sich der Umfang interner Merkmale erweitern, beispielsweise um das Datum und der Uhrzeit des Auftragseinganges und der Fristigkeit der Sendungen, also um Abhol- und Zustellfenster.
Verfahren des maschinellen Lernens können durch eine Reihe von Hyperparametern an unterschiedliche Problemstellungen angepasst werden. Eine ungünstige Parametrisierung bzw. initiale Belegung der Modellparameter kann zu schlechten Trainingsergebnissen führen, weshalb die richtige Parametrisierung sehr wichtig für das Verfahren ist.
Das Modell enthält alle Besonderheiten der betrachteten Spedition. Zur Verallgemeinerung müsste die Datenbasis mit Informationen unterschiedlicher Speditionen und weiteren Informationen (z.B. die Ergebnisse der kontinuierlichen Verkehrsmessung des Kraftfahrt Bundesamtes (KBA); vgl. [KBA 2019])) verdichtet werden.
Quellenverzeichnis
[EU 2006] Europäisches Parlament; 2006; Verordnung zur Harmonisierung bestimmter Sozialvorschriften im Straßenverkehr und zur Änderung der Verordnungen (EWG) Nr. 3821/85 und (EG) Nr. 2135/98 des Rates sowie zur Aufhebung der Verordnung (EWG) Nr. 3820/85 des Rates; Verordnung (EG) Nr. 561/2006 des Europäischen Parlamentes und des Rates
[Fard 2016] Fard, Mahdi Milani; Canini, Kevin; Cotter, Andrew; Pfeifer, Jan; Gupta, Maya; 2016; Fast and Flexible Monotonic Functions with Ensembles of Lattices; Advances in Neural Information Processing Systems 29 (NIPS 2016); Google Inc.; http://mayagupta.org/publications/FastAndFlexibleMonotonicFunctions_NIPS2016.pdf; letzter Zugriff: 03.05.2021
[KBA 2019] Kraftfahrt Bundesamt (KBA); 2019; Erhebung zur Güterkraftverkehrsstatistik inländischer Lastkraftwagen; https://www.kba.de/DE/Statistik/Kraftverkehr/kraftverkehr_node.html; letzter Zugriff: 03.05.2021
[Kingma 2014] Kingma, Diederik P.; Ba, Jimmy; 2014; Adam: A Method for Stochastic Optimization; https://arxiv.org/abs/1412.6980; letzter Zugriff: 03.05.2021
[Loukas 2020] Loukas, Serafeim; 2020; Everything you need to know about Min-Max normalization: A Python tutorial; https://towardsdatascience.com/everything-you-need-to-know-about-min-max-normalization-in-python-b79592732b79; letzter Zugriff: 03.05.2021
[Mahul 2004] Mahul, Antoine; Aussem, Alexandre; 2004; Training Feed-Forward Neural Networks with Monotonicity Requirements; Research Report LIMOS/RR-04-11; Blaise Pascal University, Clermont-Ferrand, France; https://www.researchgate.net/publication/252604793_Training_Feed-Forward_Neural_Networks_with_Monotonicity_Requirements; letzter Zugriff: 03.05.2021
[Mishura 2018] Mishura, Yuliya; Zili, Mounir; 2018; Stochastic Analysis of Mixed Fractional Gaussian Processes; ISTE Press – Elsevier, 1. Auflage; ISBN: 978-1-785-48245-8
[Murphy 2012] Murphy, Kevin P.; 2012; Machine Learning: A Probabilistic Perspectiv; MIT Press; ISBN: 978-0-262-01802-9
[Rojas 1996] Rojas, Raul; 1996; Theorie der neuronalen Netze: Eine systematische Einführung; Springer Lehrbuch; 1. Auflage; ISBN: 978-3-540-56353-2
[St. Gallen 2019] Universität St. Gallen – Institut für Supply Chain Management; 2019; Entwicklung der Transportpreise im Straßengüterverkehr; Göttingen: Cuvillier Verlag; 1. Auflage; ISBN: 978-3-736-97043-4
[Vogel 2020] Verlag Heinrich Vogel; 2020; Kraftverkehrshandbuch 2021 – Aktuelle Vorschriften für den Straßengüterverkehr im In- und Ausland; München: Springer Fachmedien; 46. Auflage; ISBN: 978-3-574-60402-7
[Windzio 2013] Windzio, Michael; 2013; Regressionsmodelle für Zustände und Ereignisse; Wiesbaden: Springer Fachmedien; 1. Auflage; ISBN: 978-3-531-15554-8
[You 2017] You, Seungil; Ding, David; Canini, Kevin; Pfeiffer, Jan; Gupta, Maya; 2017; Deep Lattice Networks and Partial Monotonic Functions; Google Inc.; https://arxiv.org/abs/1709.06680; letzter Zugriff: 03.05.2021




Um einen Kommentar zu hinterlassen müssen sie Autor sein, oder mit Ihrem LinkedIn Account eingeloggt sein.