Quantum computers are promised to dramatically change how we think about computing, what problems we can solve and to which depth we understand our environment. With unparalleled implications for applications in physics, optimization, or machine learning, it is no surprise that this exciting field attracts more and more interest not only in research but also in industry and among individuals.
Thus, it is important to understand the differences and the additional potential Quantum computers can provide. However, Quantum computing and especially Quantum entanglement, one of the key properties underpinning its power, is difficult to understand as it contradicts our everyday experiences and intuition.

To learn about complicated topics like these and to develop a basic understanding of the ideas that conflict with the way that we perceive the world around us, Serious Games – games designed for a primary purpose other than pure entertainment – can be used with the objective to explain the fundamental concepts of Quantum computing such as entanglement.

The GHZ game

Imagine that you and your two friends, Alice and Bob, have been caught by an evil wizard. As he likes to play games, he gives the three of you a riddle and promises that you are free to go if you give the correct answer.

The rules for this game are as follows:

• The three players are locked in different rooms.
• Each of you is given a piece of paper asking either for a color or for a shape.
• If asked for a color you can write red or blue on the paper, if asked for a shape you can chose either a star or a rectangle.
• The wizard will either ask all three of you for a color or two for a shape and one for a color.
• If all three are asked for a color, you win if red was answered an even number of times.
• If two players are asked for a shape and one for a color, you win if combined an uneven number of players answered with red or star depending on the question they were asked.
• You do not know what your friends were asked and what they answered and have no possibility to communicate.

Shortly before the wizard captured you, you had the chance to formulate a strategy on how to proceed. You and your friends agreed that if asked for a shape, all of you will answer with star, and if asked for a color, all of you will answer with red. However, after a while you realize that this solution only works in three out of four possible cases, as illustrated below.

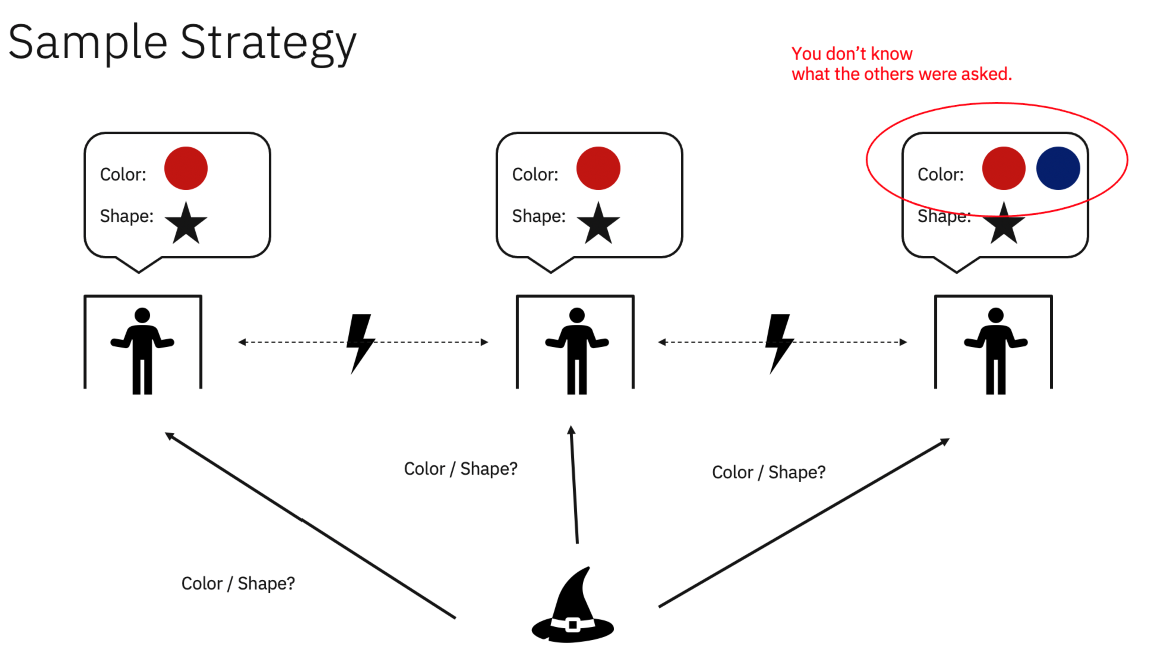
In fact, classically, it is impossible to find a perfect solution using pre-agreed values. The highest winning probability that can be achieved this way is 75%.

However, when using Quantum entanglement, it becomes possible to develop a perfect solution for this hopeless situation. If you want to learn more about this and find the solution yourself, you can play the GHZ game using the interactive notebook “GHZ game” on [1]. Here, we will provide a short summary.

Quantum entanglement results in a strong dependency between qubits, allowing to store information that could not be stored on three independent qubits. If you and your friends each have one of three entangled qubits, it enables you to give coordinated answers without the n

eed to communicate. Whether the wizard asks you for a shape or a color translates into reading the qubit in a different measurement base for each case. To retrieve information in a specific measurement base, we add additional gates to the target qubit before the quantum measurement operation.

Below you find an example. In the first part of the Quantum circuit, the three qubits are being entangled, resulting in the so-called GHZ state. Then, after the grey barrier, a measurement follows according to the question asked. In this example, the first person (top wire) is asked for a color and the other two are asked for a shape. Using the appropriate Quantum circuit, you will always receive one of the correct answers, no matter which question the wizard asked to whom. This means that on an ideal quantum computer, we will win the game with 100% probability.

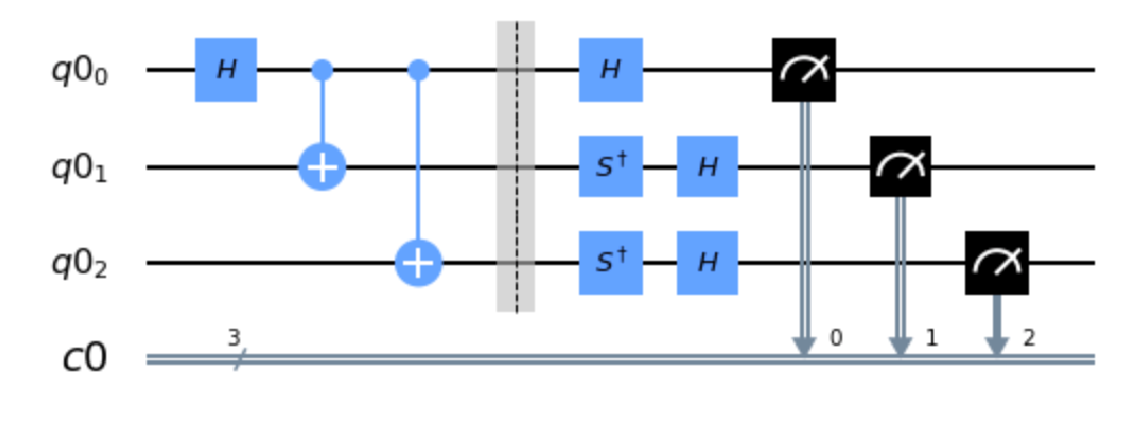
Playing the GHZ game on real Quantum computers

Does that mean you have outsmarted the evil wizard? Unfortunately, not yet. For the above solution to work reliably, we would need a perfect Quantum computer, which currently does not exist. Today’s Quantum computers are imperfect, meaning that they are subject to a number of error sources and noise that render the outcomes of a Quantum algorithm partially incorrect. For this reason, we play the GHZ game mainly on a simulator.

However, there are some tricks to beat the wizard on a noisy Quantum computer too!

First of all, let us identify the reasons why the results on a real system are different from those on a simulator. Remember that a Quantum algorithm consists of a Quantum circuit like the one above, where on multiple qubits different gates are applied over time.

Mainly, we can distinguish two groups of issues. First, there are imperfections and errors that occur at different stages of executing a Quantum circuit. In some cases, the system can fail to accurately prepare qubits in their ground state before the algorithm starts. Similarly, gates, which manipulate the Quantum state of a qubit, can perform inaccurate transformations leading to accumulating errors. Ultimately, errors might occur when measuring the state of a qubit at the end of an algorithm, an operation which forces them to collapse into either of its two basis states. When instead of the expected classical state another one is randomly returned, we refer to it as measurement error.

Second, there are independent physical effects that corrupt the state of a Quantum system over time. Since Quantum states are very fragile, they would require outer-space conditions to persist. Even though current devices, such as the IBM Q System One, operate close to absolute zero temperature, we cannot yet isolate the systems to the extent that would be necessary. Due to small interactions with the environment and between qubits, the Quantum states held in the system slowly lose their Quantum properties, which is what we refer to as decoherence.

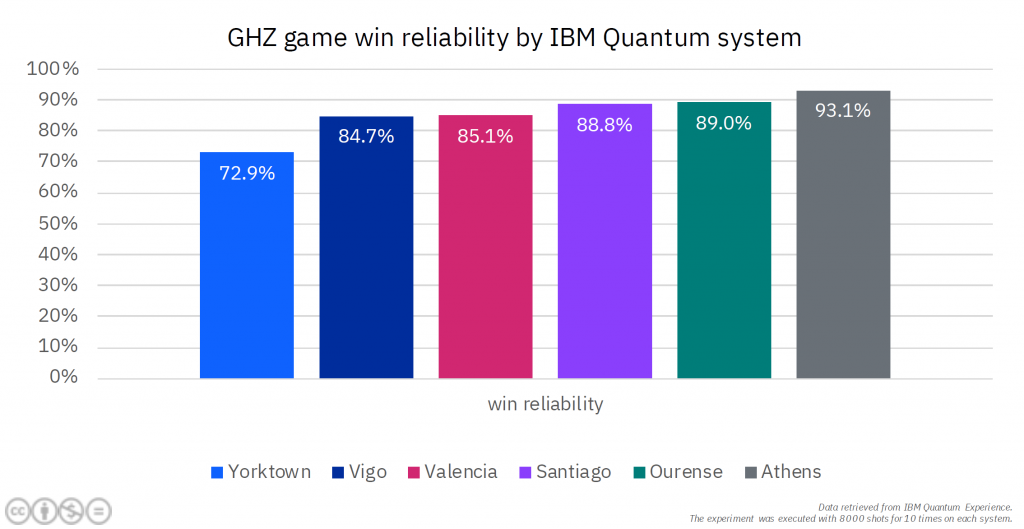
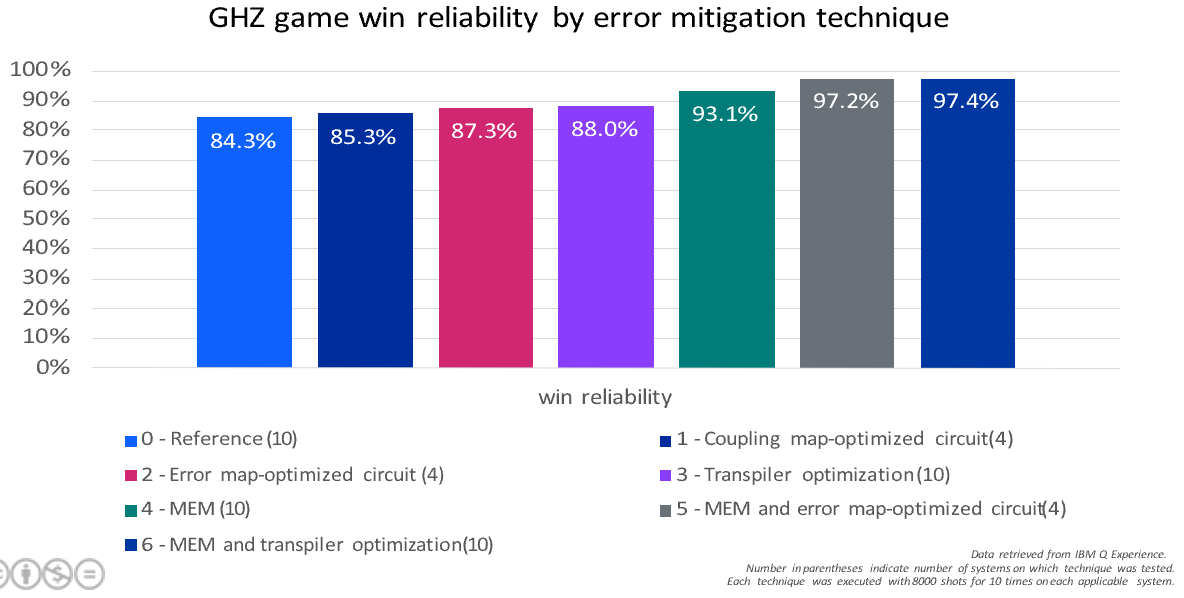
To quantify these effects, we introduce a metric that tells us how reliably we can win the game. In an ideal Quantum world, this value would be 100%, indicating all of the returned results are correct so that we always solve the riddle. Due to the present errors, we found that on average, the fidelity achieved on selected IBM Q real Quantum devices only is 84.3%, 15.7 percent points less than on the ideal simulator. Even though this does not sound too much, imagine being locked by the wizard and failing to escape – or even worse, imagine trying to reliably decode chemical properties of a molecule in order to develop a new drug!

Luckily, plenty of methods are being researched and developed that can help us to improve the accuracy of our results.

Think about the second category of error sources. In principle, the longer an algorithm runs on a system the greater will be the effect of decoherence. Furthermore, each additional gate introduces additional error due to its unprecise transformation. Thus, reducing the number of gates is key.

Now, if we wish to run the GHZ game circuit on a real device, we need to consider the physical layout of the qubits of the Quantum computer. If it does not match how we connect the qubits through the gates in our circuit, additional gates are added before the execution that maintain the semantics of the circuit while transforming it to correspond to the device’s properties on the hardware level. Hence, if we pick the qubits in our circuit in a way that matches the alignment of the physical qubits, we can omit this overhead. In fact, this coupling map-adaptive optimization returned a win reliability of 85.3% on the four devices tested, an improvement of one percent point.

Furthermore, consider that the gate and measurement errors can greatly vary from one qubit to another even within the same machine. In a similar way to above, let us, thus, try to pick qubits for our circuit that fit the physical layout of the device and among these have the lowest gate and readout error rates. Using this error map-adaptive approach we win with 87.3% certainty; another two percent points up.

Both of these steps can be done automatically in Qiskit, the software that we use to execute Quantum algorithms, applying the so-called transpiler optimization. The transpiler is the engine that translates our logical Quantum circuits into those that are executable on our target Quantum computer. Its strongest configuration considers aspects far beyond the aforementioned two. And indeed, using this feature we receive a win reliability of 88.0%.

Now, the reliability is still not there where we need in order to defeat the wizard with confidence. Let us therefore use a more advanced technique, which is called measurement error mitigation. By experimentally examining the behavior of our Quantum computer, we can statistically deduce how strong the influence of measurement errors is in our results – and can calculate them out after we retrieved them! Applying this technique on our results from the error map-optimized circuit and the one optimized by our transpiler, we achieve a tremendous reliability of more than 97% and almost certainly win the game.

If you wish to try these methods on a real quantum computer yourself, you can do so by visiting the notebook “GHZ game on real devices” on [1].

Besides the discussed techniques, which represent only a few examples under the large umbrella of Quantum error mitigation, there is even a fully developed theory that can ensure algorithms to reliably produce results that are completely accurate, referred to as Quantum error correction. Even though this is not feasible to implement on current devices, it gives you a glimpse of the future power of Quantum computers. Using entanglement and our mitigation strategies, the wizard better be prepared!

Sources, References and further reading:

[1] https://github.com/JanLahmann/Fun-with-Quantum

Hands-on interactive notebooks for the GHZ game and Quantum error mitigation: https://github.com/JanLahmann/Fun-with-Quantum

IBM Quantum Experience: https://quantum-computing.ibm.com

Theoretical foundations of the GHZ state: Greenberger, D. M.; Horne, M. A.; Zeilinger, A. (1989): Going Beyond Bell’s Theorem. Fundamental Theories of Physics, Vol.37, pp.69-72.

Introduction to Quantum measurement error mitigation in the Qiskit Textbook: https://qiskit.org/textbook/ch-quantum-hardware/measurement-error-mitigation.html

Hands-on journey to Quantum computing with IBM: https://medium.com/@jan.lahmann/hands-on-journey-to-quantum-computing-with-ibm2487f0b2e10b

Playful introduction to the concepts of superposition and entanglement: https://digitaleweltmagazin.de/2020/03/06/ein-spielerischer-einstieg-in-quantum-computing/ 

Exploring Quantum capabilities using a Raspberry Pi and a 3D printer: https://digitaleweltmagazin.de/2021/01/08/rasqberry-oder-was-hat-ein-raspberry-pi-mit-einemquantencomputer-zu-tun/