Abstract

Klassische Monte-Carlo Simulationen besitzen eine Varianz \(Var(X)/N\) mit der zugrunde liegenden zu simulierenden Zufallsvariable X. Nun wird berichtet, dass eine quadratische Verbesserung der Konvergenz und eine von X unabhängige Varianz möglich ist, wenn die Simulation auf einem Quantencomputer durchgeführt wird. Wir wollen aufzeigen, wie dieser Vorteil der Quantum Computer möglich ist, und damit Einblick geben, was wir zu erwarten haben.

Motivation & Kontext

Die alles bestimmende Frage, welche jeder Aussage einer Quanten-Überlegenheit vorweggenommen werden muss, sollte am besten gleich zu Anfang angesprochen werden, um nicht den Eindruck zu vermitteln, man sei realitätsfern auf seinem Elfenbeinturm verhaftet. Jedem brennt die eine Frage unter dem Nagel, werden wir bald in den Genuss dieser neuen Kraft kommen können? Das Forschungslabor der IBM in Zürich, Goldman Sachs und die Universität von Maryland, USA, haben sich dieser Frage angenommen und die Anzahl von (fehlertoleranter) Qubits sowie der Operationen für die Bepreisung einer Option (TARF Derivate) berechnet und sie gegenüber der Rechenzeit gestellt, in der man nach heutigen Maßstäben rechnen möchte: 1 Sekunde [1]. Dieses ergab, dass die Rechengeschwindigkeit der teuersten Operationen bei 10MHz liegen muss, jedoch wird derzeit gemutmaßt, dass lediglich 10kHz erreicht werden können[2].

Es besteht aus dieser Sicht Zweifel an der Anwendbarkeit, und doch sollte man gerade im Bereich neuer Technologien vorsichtig sein, denn der Stand der Technik ändert sich rasant. In der Zwischenzeit – also bevor „richtige“ Quantencomputer mit hunderte fehlertoleranter Qubits zur Verfügung stehen – ist man bestrebt, Algorithmen zu finden, welche explizit jetzige oder nächste Generation von Quantenprozessoren nutzen möchten. Diese werden auch NISQ (Noisy Intermediate Scale Quantum) Prozessoren genannt[3].

Nicht ohne Grund hat sich das oben genannte Konsortium ein Problem ausgesucht, dass eine Monte-Carlo Simulation als Grundlage hat. Diese Methode ist ein in Industrie und Wissenschaft häufig eingesetztes stochastisches Verfahren zur nummerischen approximation wichtiger Kennzahlen. Durch Mittelwertbildung über eine sehr große Anzahl an zufällig generierten Experimenten ermöglichen sie eine Schätzung der gesuchten Größe.

Wie effizient und präzise diese approximation ist, wird durch die Varianz der zugrundeliegenden Zufallsvariable und die Stichprobengröße bestimmt.  Um die Präzision der Schätzung zu verbessern, versucht man häufig, die Varianz der verwendeten Zufallsvariable zu reduzieren, ohne dabei das Ergebnis der Durchschnittsbildung zu verändern. Eine der bekanntesten Methoden ist der Metropolis–Hastings Algorithmus, welcher in die Klasse Variance Reduction Methoden fällt.

In der Tat haben sich in letzter Zeit gleich mehrere Fachbeiträge dem Thema Monte-Carlo ähnlicher Methoden für Quanten Computer angenommen [4-8]. Daraus ergibt sich die These, dass die Berechnung von Erwartungswerten unter Transformationen sich quadratisch besser \approximieren lassen, als es für Klassische Computer der Fall ist. Diese Erkenntnis scheint auf einer sehr wichtigen Eigenschaft der Quanten Mechanik zu fußen, der Quantenverschränkung. Im Quantum Computing gibt es zwei wesentliche und sehr bekannte Algorithmen, die die theoretische Überlegenheit von Quantenberechnungen in den 1990er Jahren belegten, die Primfaktorzerlegung [9, 10] und das effizientere Suchen einer Datenbank [11]. Es ist damit nicht verwunderlich, dass beide Prinzipien in diesem Trick genutzt werden, namentlich der Amplitude Amplification[12].

Jedoch stellt sich die Frage, wie lässt sich diese „quadratische“ Quantenüberlegenheit denn mit klassischen Algorithmen vergleichen? Dies lässt sich jedoch so direkt nicht beantworten. Beispielsweise könnte man die Anzahl der Anwendungen der Simulationsalgorithmen für den klassischen und auch den quantenartigen Fall ermitteln und diese dann mit der erreichten Präzision in Relation setzen. Diese Ansicht ist allerdings nicht unumstritten. Während im klassischen Verfahren mit jeder einzelnen Anwendung der Simulation eine Realisation erzielt wird, lädt Quantenalgorithmus die vollständige Verteilung in den Quantenzustand.  Man sieht also schon hier, dass eine direkte Vergleichbarkeit nicht gegeben ist.

In unserer Arbeitsgruppe wurde gezeigt[7], dass Monte-Carlo ähnliche Methoden auf dem Quanten Computer nicht nur das oben genannte Amplitude Estimation, sondern ebenso eine Ein-Qubit-Messung als Alternative genutzt werden kann, die konsequenter Weise keine quadratische Verbesserung der Präzision mit sich bringt. Eine der Behauptungen dieser Arbeit ist jedoch, dass Quantenalgorithmen für Monte-Carlo ähnliche Methoden eine Varianzreduktion erreichen können, in der Tat wird die Varianz einer Bernoulli-Verteilung identifiziert. Was bedeutet dies aber konkret? Klassische Monte-Carlo Simulationen besitzen die Varianz  mit der zugrunde liegenden Zufallsvariable , die simuliert wird. Nun wird berichtet, dass die Varianz unabhängig von  ist, wenn die Monte-Carlo Simulation auf dem Quantencomputer durchgeführt wird.

Wir zeigen, dass dieses faszinierende Detail in der Tat für beide Ansätze gleichermaßen gilt, der Anwendung der Amplitude Estimation mit dem quadratischen Vorteil und der Ein-Qubit-Messung für heutige fehlerhafte Quanten Prozessoren. Die Konsequenzen dieser Erkenntnis würden viele Industrien berühren, an denen hoch-komplexe Monte-Carlo Modelle berechnet werden. Dazu gehören Wettermodelle, Chemische Reaktionen, Medizinische Forschung, Finanzen & Märkte, Versicherungen und Logistik, um ein paar zu nennen.

Wir wollen mit steigender Komplexität den Leser in die Höhle der Quantenalgorithmen locken. Die Einführung sollte die wichtigsten Aussagen beinhalten, um eine Idee zu bekommen, was Quantencomputer für die Berechnung von Erwartungswerte machen können und wie realistisch dies auch ist. Das nächste Kapitel soll es mit dem Wissen über Quantenalgorithmik noch gemächlich angehen, jedoch unsere Kernaussage – die der quadratischen Konvergenzsteigerung und der Varianz Reduktion – mit mehr Mathematik untermauern. Wir wollen nicht in den Algorithmus des Amplitude Estimations tauchen, denn das sprengt diesen Bericht bei Weitem. Das darauffolgende Kapitel geht deutlich tiefer in die Quantenalgorithmik und zeigt auf, wie man konkret einen vergleichsweise einfachen – aber nicht trivialen – diskreten stochastischen Prozess auf einem Quantencomputer modelliert. Dieses Kapitel ist für all jene, die eine Idee brauchen, um in den Ansatz Vertrauen zu gewinnen. Das letzte Kapitel widmet sich der Zusammenfassung sowie der Diskussion und soll für den interessierten Leser wieder verständlich sein.

Der Quantenvorteil beim Monte-Carlo Sampling

Nun wollen wir einige der obigen Aussagen präzisieren. Sei \(X\) eine Zufallsvariable und eine Transformation (\(f:\mathbb{R}\rightarrow\mathbb{R}\)), dann wissen wir (1):

\begin{equation}\label{eqn:1}\left|\mathbb{E}\left[f\left(X\right)\right]-\frac{1}{N}\sum_{i=1}^{N}f\left(X_i\right)\right|^2\le\frac{Var\left(f\left(X\right)\right)}{N}\end{equation}
wobei wir \(X_i\) \((i=1\ldots N)\) als identisch und unabhängige verteilte Zufallsvariablen mit derselben Verteilung wie  \(X\) annehmen. Die Summe ist lediglich der \approximierte Wert, welcher durch die Monte-Carlo Simulation ermittelt wird, mit \(N\)  Simulationen. Die Aussage, die sich nun hinter den Arbeiten von Montanaro [4], Rebentrost et al.[5], und Wörner et al.[8,13,14] verbirgt, ist, dass dieser Fehler (2):
\begin{equation}
\label{eqn:2}
\left|\mathbb{E}\left[f\left(X\right)\right]-\widetilde{a}\right|^2\le\frac{C}{M^2}
\end{equation}
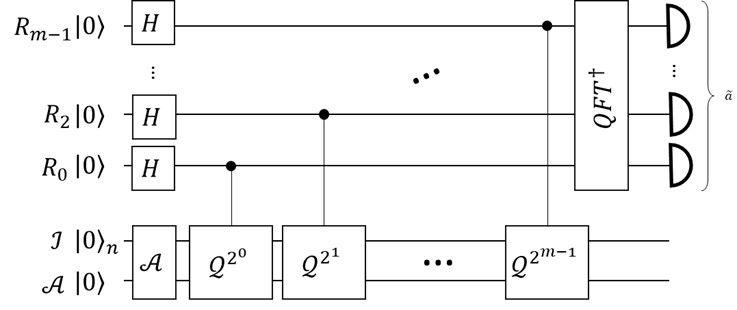
beträgt, wobei \(\widetilde{a}\) die Messung nach der Amplitude Estimation[12] beziffert. Mit etwas Rücksicht auf die Tatsache bezogen, dass \(N\)  und \(M\)  zwei unterschiedliche Bedeutungen haben, legt dies dennoch nahe, dass es eine Methode gibt, die Anzahl von Anwendungen des Monte-Carlo Algorithmus reduzieren kann. Die Sache ist selbstverständlich nicht offensichtlich, denn was wirklich passiert, ist dass m neue Auslese Qubits in das System eingeführt werden und es (\(M={\mathcal{O}(2}^m)\)) Anwendungen des Monte-Carlo-ähnlichem Algorithmus gibt, mit dem Messfehler wie in Gleichung (2) beschrieben. So wird die Anzahl von Anwendungen miteinander verglichen, und zwar auf sehr unterschiedlichen Architekturen. Dennoch macht dies Sinn, obwohl man diesen Hintergrund nicht vergessen sollte.

\begin{array}{c|c|c|c}
Methode & Fehler & n-Algo auf  Quant. Proz. & n-Experimente \\ \hline
Amplitude Estimation & \left|\mathbb{E}\left[f\left(X\right)\right]-\widetilde{a}\right|\le\frac{\sqrt 3}{M} & M & * \\
Ein-Qubit-Messung & \left|\mathbb{E}\left[f\left(X\right)\right]-\widetilde{e}\right|\le\frac{1}{2\sqrt N} & 1 & N \\
Monte-Carlo & \left|\mathbb{E}\left[f\left(X\right)\right]-\widetilde{e}\right|\le\frac{Var\left(f\left(X\right)\right)}{\sqrt N} 0 & N\end{array}

Tabelle 1: Der Vergleich der Fehler. Die ersten beiden Einträge sind Quantenalgorithmen, die letzte ist die bekannte Monte-Carlo Methode, ohne Varianz Reduktion. Die Amplitude Estimation* muss nur ein paar Mal ausgeführt werden um bei einer Erfolgswahrscheinlichkeit von \(\pi^2/8\) statistische Sicherheit zu erhalten, wohingegen beide andere Verfahren N Mal wiederholt werden. Man sieht hier recht eindrucksvoll, dass Quantenalgorithmen einen Vorteil bringen können.

Die Frage, die in diesem Zusammen noch nicht erklärt wurde, ist nun, wie sieht ein Monte-Carlo Algorithmus aus, welcher auf einem Quanten Computer ausgeführt wird? Dazu wurden Arbeiten in den letzten Jahren verfasst[7,8,13,14], welche Konstruktionen unter Anwendungen erklären. Der einfachste Erklärungsansatz umfasst, dass eine die Zufallsvariable \(X\) auf (k>0) Werte diskretisiert wird und mit der Wahrscheinlichkeitsdichte in einen Quanten Zustand gebracht wird. Anschließend wird die Transformationsfunktion \(f\)  auf ein extra Qubit angewandt, so dass die Anwendung des Amplitude Estimation die Summe aus Wahrscheinlichkeiten und der Transformationsfunktion ,,ausgelesen“ wird. Konkret sei die Wahrscheinlichkeitsdichte \(p(i)=\mathbb{P}([X^\prime=x_i)]) ((x_i\in(\{0, \ldots, k-1)\})\) der diskretisierten Zufallsvariablen \(X\) berechnet, wodurch ein Quantenzustand (3):
\begin{equation} \label{eqn:3} \mathcal{R}\left|0\right\rangle_n=\left|\psi\right\left=\sum_{i=0}^{k-1}{\sqrt{p_i}\left|i\right\left} \end{equation}
erzeugt wird. Sodann wird ein neues Qubit hinzugefügt auf dem im Anschluss eine Operation ausgeführt wird, welche den vorherigen Zustand überführt in (4): \begin{equation} \label{eqn:4} F\left|\psi\right\rangle\left|0\right\rangle=\sum_{i=0}^{k-1}{\sqrt{p_i}\left|i\right\rangle\left(\sqrt{1-f^{\prime\left(i\right)}}\left|0\right\rangle+\sqrt{f^{\prime\left(i\right)}}\left|1\right\rangle\right)} \end{equation}
mit \(f^\prime\left(i\right)=f(x_i)\), so dass \(\mathcal{A}=F\mathcal{R}\) eine Anwendung des Algorithmus ist. Die Anwendung des Amplitude Estimation schätzt den Wert \(a=\left\langle\psi_1\middle|\psi_1\right\rangle\) mit \(\left|\psi_0\right\rangle=\sum_{i=0}^{k-1}{\sqrt{p_i}\sqrt{1-f^{\prime\left(i\right)}}\left|i\right\rangle\left|0\right\rangle}, \left|\psi_1\right\rangle=\sum_{i=0}^{k-1}{\sqrt{p_i}\sqrt{f^{\prime\left(i\right)}}\left|i\right\rangle\left|1\right\rangle}\), somit gibt es die orthogonale Zerlegung \(F\mathcal{R}\left|0\right\rangle_n\left|0\right\rangle=\left|\psi_0\right\rangle+\left|\psi_1\right\rangle\). Anstatt Amplitude Estimation anzuwenden, wurde eine NISQ freundliche Alternative aufgewiesen[7], indem man eine Ein-Qubit-Messung auf dem letzten Qubit durchführt und die Wahrscheinlichkeit schätzt, in der der Zustand 1 vorkommt. Nun wollen wir zeigen, dass in diesen beiden Mess-Ansätzen auch ein weiterer Quanteneffekt in der Berechnung von Erwartungswerten auftritt: eine Varianz Reduktion unabhängig von der Varianz der Zufallsvariablen X oder dessen Diskretisierung \(X^\prime\).

Betrachten wir die Gleichung(4) und führen eine Ein-Qubit-Messung z.B. mit einer Pauli \(\sigma_z=P_1+P_{-1}=\left|0\right\rangle\left\langle0\right|-\left|1\right\rangle\left\langle1\right|\) Observablen durch. Nur das Ergebnis -1 interessiert uns, so dass wir die Observable \(P_{-1}\) etwas genauer betrachten. So erhalten wir (5):
\begin{align} \label{eqn:5} \left\langle P_{-1}\right\rangle&=Tr\left(\left|1\right\rangle\left\langle1\right|\mathcal{A}\left|0\right\rangle_{n+1}\right)\\ &=\sum_{i=0}^{k-1} p_i f^{\prime\left(i\right)} \nonumber\\ &=\sum_{i=0}^{k-1}f\left(x_i\right)\mathbb{P}\left[X^\prime=x_i\right] \nonumber\\ &=\mathbb{E}\left[f\left(X^\prime\right)\right] \nonumber\\ &\approx\mathbb{E}\left[f\left(X\right)\right] \end{align}
Jedoch ist die Varianz dieser Messung nicht abhängig von der Zufallsgröße \(X^\prime\), wie es für Monte-Carlo Methoden der Fall wäre. Stattdessen gilt die Varianz der Observablen \(P_{-1}\). Für die zugehörige Zufallsvariable \(Y_P\) der Messung gilt nämlich (6):
\begin{equation} \label{eqn:6} Y_p\sim Ber\left(p\right) \end{equation}
mit \(p=\mathbb{E}\left[f\left(X\prime\right)\right]\), daher \(Var\left(Y_P\right)=\Delta P_{-1}=p\left(1-p\right)\). Dieses recht einfache Ergebnis resultiert aus \(\left\langle P_{-1}^2\right\rangle=0^2\left(1-p\right)+\left(-1\right)^2p=p\) und somit \(\Delta P_{-1}=\left\langle P_{-1}^2\right\rangle-\left(\left\langle P_{-1}\right\rangle\right)^2=p-p^2=p\left(1-p\right)\). Vergleichend mit Gleichung (1) ist offensichtlich, dass die Statistiken der Zufallsgrößen X oder deren diskretisierte Zufallszahl \(X\prime\) keinerlei Einfluss haben.

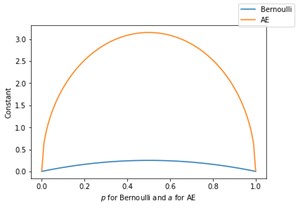
Diese Tatsache gilt ebenso für die Amplitude Estimation wie durch Gleichung(2) deutlich gemacht. Die Konstante (C>0) ist ebenfalls unabhängig von diesen beiden Zufallsvariablen, konkret gilt \(C=2\pi j\sqrt{a\left(1-a\right)}+\frac{j^2\pi^2}{M}\), für jedes beliebige (j>0). Man betrachte die Abbildung 1, welche die Konstanten beider Methoden zeigt. Zusammenfassend gibt die Tabelle 1 eine Übersicht.

Quantum-Brute-Force für eine Irrfahrt

Wir sehen aus diesen Überlegungen, dass Quantencomputer vor allem in einer Sache großartig sind: große Summen zu bilden[15]. Diese Eigenschaft ist gerade in der Berechnung von Erwartungswerten hilfreich, wie wir gerade gesehen haben. Nicht umsonst wurde der vorgeschlagene Ansatz „Quantum-Brute-Force“[7] genannt, denn man encodiert die gesamte Zufallsvariable, also alle möglichen Realisationen und deren Wahrscheinlichkeiten. Doch jeder, der Monte-Carlo Methoden bereits angewandt hat, weiß zu berichten, dass gerade das Fehlen dieser Möglichkeit die Methode attraktiv macht. Hier besteht größtenteils die Problematik des Quantenansatzes. Die nötigen Werte der Wahrscheinlichkeitsdichte in Quantenzustände zu übertragen, kann für sehr komplexe diskrete Zufallsvariablen so groß sein, dass die sog. State Preparation[16-20] die realistische Anwendung unmöglich machen würde. Konkret bedeutet dies, dass für die Erstellung des Zustandes (3) auch eine von der Zahl  abhängige Anzahl elementarer 2-Qubit Quantengatter (c-not) angewandt werden muss. Um dieses Problem jedoch zu umgehen, gibt es interessante Ansätze: variationelle Methoden[21-24], generative Methoden[25] und konstruktive Methoden[7,15,26]. Variationelle Methoden bedienen sich eines Quantum-Klassisch Hybridalgorithmus, um meist durch ein Gradienten-Verfahren nah an die gewünschte Verteilung zu kommen. Ähnlich sind Generative Methoden zu verstehen, jedoch wird hier der Fokus auf Deep Learning Netzwerke gelegt, insbesondere deren Quantum-Varianten.

Aus eigener Praxis stellen wir eine konstruktive Methode vor[7]. Anhand eines Beispiels soll erläutert werden, wie eine sog. korrelierte Irrfahrt erzeugt wird.

Definition. Eine korrelierte Irrfahrt (X_n) ist ein diskreter stochastischer Prozess und besitzt folgende Eigenschaften. \(\mathbb{P}\left[X_1=+1\right]=\mathbb{P}\left[X_1=-1\right]=\frac{1}{2}\) sowie
\begin{align*} \mathbb{P}\left[X_n=+1|X_{n-1}=+1\right]=p_n,\quad \mathbb{P}\left[X_n=-1|X_{n-1}=+1\right]={1-p}_n \\ \text{ und } \mathbb{P}\left[X_n=-1|X_{n-1}=-1\right]=q_n,\quad \mathbb{P}\left[X_n=+1|X_{n-1}=-1\right]={1-q}_n \end{align*}
für Folgen \(q=\left(q_2, q_3,q_4, \ldots\right), p=\left(p_2,p_3,p_4, \ldots\right)\).

Nun wollen wir den Prozess bis zu einer Länge (n>1) als Wahrscheinlichkeitsdichte berechnen, es gibt daher (le2^n) Pfade. Da dieser Prozess autokorreliert ist, insbesondere für den Spezialfall q=p gilt \(\mathbb{E}\left[\left(X_n-X_{n-1}\right)\left(X_{n+m}-X_{n+m-1}\right)\right]=\left(2p-1\right)^m\), siehe Enriquez[27]. Somit ist die Berechnung von der Wahrscheinlichkeitsdichte nicht trivial. Mit einer Monte-Carlo Simulation lassen sich natürlich Realisierungen und deren Wahrscheinlichkeiten errechnen, und die Definition gibt die Regel an, wie die Vorwärtssimulation durchgeführt werden muss. Diese Idee kann nun elegant in einen Quantenalgorithmus umgesetzt werden. Es bedarf für die Länge n dieselbe Anzahl an Qubits und der erste Schritt wird durch einen Hadamard Gatter in die Superposition gebracht (7) \begin{equation} \label{eqn:7} H\left|0\right\rangle=\frac{1}{\sqrt2}\left|0\right\rangle+\frac{1}{\sqrt2}\left|1\right\rangle. \end{equation}
Wir identifizieren den Grundzustand mit dem Inkrement -1, behaften diesen mit der Amplitude \(1/\sqrt{2\}), welches der Wahrscheinlichkeit \(1/2\) entspricht, und identifizieren analog den angeregten Zustand mit +1. Nun führen wir einen weiteren Qubit und kontrollierte Rotationen (um die y-Achse) ein, so dass die Wahrscheinlichkeiten den (q_2, p_2) entsprechen. Dadurch erhalten wir (8)\begin{align} \label{eqn:8} H\left|0\right\rangle\left|0\right\rangle =\frac{1}{\sqrt2}\left|0\right\rangle\left|0\right\rangle+\frac{1}{\sqrt2}\left|1\right\rangle\left|0\right\rangle \nonumber \\ \rightarrow\frac{1}{\sqrt2}\left|0\right\rangle\left(\cos{\theta_{q_2}}\left|0\right\rangle+\sin{\theta_{q_2}}\left|1\right\rangle\right) + \frac{1}{\sqrt2}\left|1\right\rangle\left(\cos{\theta_{p_2}}\left|0\right\rangle+\sin{\theta_{p_2}}\left|1\right\rangle\right) \end{align}
so dass \(\cos{\theta_{q_2}}=\sqrt{q_2}\) und \(\sin{\theta_{p_2}}=\sqrt{p_2}\). Würden wir nun Messungen auf beide Qubits anstellen und deren Statistiken sammeln, so würden nach Tabelle 2 die Werte ermittelt.

Man möge sich kurz klar machen, wie diese Konstruktion funktioniert, dann argumentieren wir, dass man dieses Verfahren auch -Mal wiederholen kann. Einen Quantenschaltkreis könnte man ebenfalls einfach beschreiben, siehe Abbildung 3.

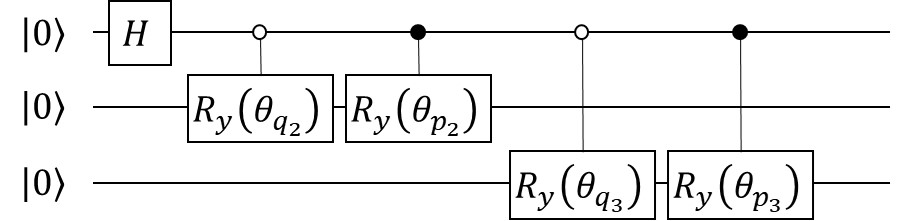
Nach n Schritten haben wir daher \(2^n\) Äste des Quantenzustands, der Basisvektor zeigt daher auf, wie die Irrfahrt aussieht. Ein Beispiel: gegeben sei der Basisvektor \(|01001100101011111011011\rangle\) so können wir die Irrfahrt ablesen, sie lautet
\begin{equation*} -1,+1,-1,-1,+1,+1,-1,-1,+1,-1,+1,-1,+1,+1,+1,+1,+1,-1,+1,+1,-1,+1,+1 \end{equation*}
und in Summe haben wir 5. Mit diesem Verfahren ist es daher möglich, die Wahrscheinlichkeiten zu erzeugen, die passend sind zu dem stochastischen Prozess.

Um das Verfahren abzuschließen, zeigen wir zudem auf, wie man Gleichung(4) bzw. Operator (F) erzeugen kann. Dazu weisen wir auf ein Verfahren hin[7] , welches ermöglicht, die charakteristische Funktion zu berechnen. Zuerst wird ein Akkumulator Qubit in das System hinzugefügt. Wir erinnern uns, in jedem Schritt wurde eine Rotation angewandt (außer der ersten, dort nutzten wir ein Hadamard Gatter). Nun nutzen wir ein kontrolliertes Phasengatter vom ersten Qubit – bedingt auf dem Grundzustand – und dem Akkumulator-Qubit als Ziel, mit der Aktion, eine relative Phase -1 zu erzeugen. Ein analoges kontrolliertes Phasengatter – nun bedingt auf den angerengten Zustand – soll die relative Phase +1 auf dem Ziel Qubit erzeugen. Wiederholen wir dieses Verfahren nun auf allen Qubits, so stellen wir fest, dass wir eine Summe der einzelnen Realisationen von \(X_1, X_2,\ldots, X_n\) in der relativen Phase haben. Für unser obiges Beispiel aus Gleichung(8) erhalten wir
\begin{align} \label{eqn:9} \frac{1}{\sqrt2}\cos{\theta_{q_2}}\left|00\right\rangle\left(\frac{1}{\sqrt2}\left|0\right\rangle+\frac{1}{\sqrt2}e^{i\left(-1-1\right)}\right) \nonumber\\ +\frac{1}{\sqrt2}sin{\theta_{q_2}}\left|01\right\rangle\left(\frac{1}{\sqrt2}\left|0\right\rangle+\frac{1}{\sqrt2}e^{i\left(-1+1\right)}\right) \nonumber\\ +\frac{1}{\sqrt2}\cos{\theta_{p_2}}\left|10\right\rangle\left(\frac{1}{\sqrt2}\left|0\right\rangle+\frac{1}{\sqrt2}e^{i\left(+1-1\right)}\right) \nonumber\\ +\frac{1}{\sqrt2}\sin{\theta_{p_2}}\left|11\right\rangle\left(\frac{1}{\sqrt2}\left|0\right\rangle+\frac{1}{\sqrt2}e^{i\left(+1+1\right)}\right) \end{align}
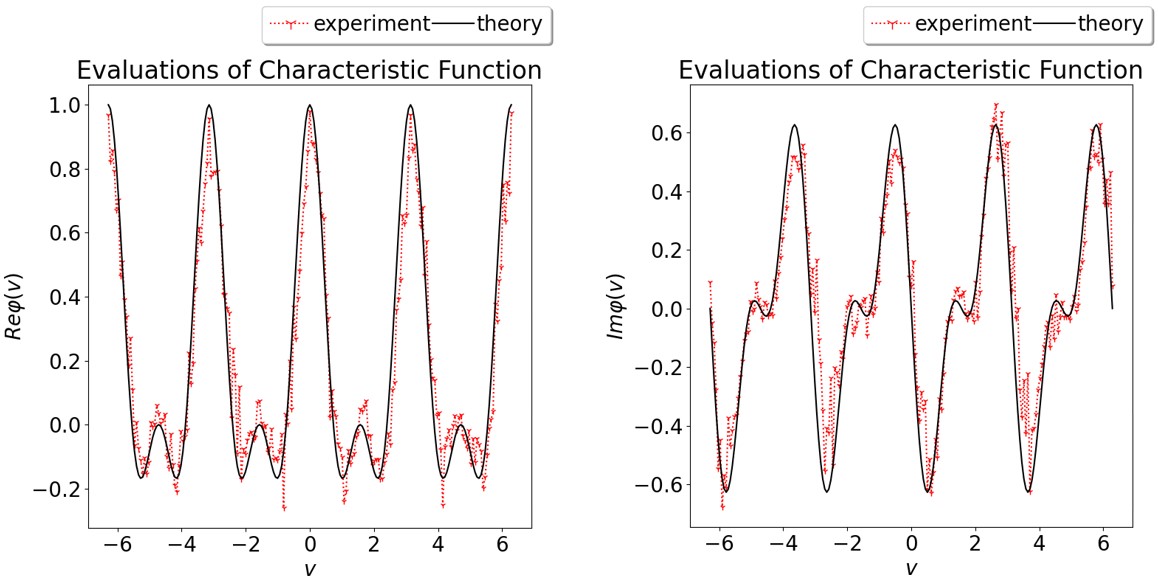
Mit einer Pauli X Messung erhält man nun \(\mathbb{E}\left[\cos{X_n}\right]\) und mit einer Pauli Y Messung \(\mathbb{E}\left[\sin{X_n}\right]\). Man kann nun folgendes tun: mit \(var\phi_{X_n}\left(v\right)=\mathbb{E}\left[\cos{\left(vX_n\right)}\right]+i\mathbb{E}\left[sin{\left(vX_n\right)}\right]\) können wir das charakteristische Polynom errechnen, wenn wir je \(v\in\mathbb{R}\) zwei Experimente ausführen. Das Ergebnis nach Konvergenz, welche unabhängig von der Varianz von (X_n) ist, kann man der Abbildung 4 entnehmen. Damit kann man zeigen, dass die Methode durchaus auf heutigen Prozessoren anwendbar ist. Zu Details verweisen wir auf unsere Arbeit [7].

Zusammenfassung & Diskussion

Wir halten daher zunächst fest, dass Quanten Computer hervorragend sind, wenn es um die Berechnung von großen Summen geht. Jedoch müssen Zustände erzeugt werden, die einen großen Aufwand mit sich bringen. Wenn dies aber gelänge, können Operationen wie die von (4), gefolgt von der Amplitude Estimation oder die Ein-Qubit-Messung angewandt werden, um schneller an ein Ergebnis zu kommen.

Somit wollten wir in diesem Bericht auf die Tatsache aufmerksam machen, dass Quanten Computer einen Vorteil bei Monte-Carlo ähnlichen Simulationen aufweisen können. Eine der bedeutendsten Steigerungen wird durch die Amplitude Estimation erreicht, welche aber derzeit nicht für NISQ Prozessoren in Frage kommt. Es wurde zwar eine NISQ freundlichere Alternative vorgestellt, jedoch kann sie den Zugewinn von Leistung nicht erreichen. Beide Verfahren können jedoch mit dem Vorteil aufwarten, dass deren Varianz nicht von den zugrundeliegenden Zufallsvariablen abhängt. Damit erfüllen beide eine Varianz Reduktion. Gegeben der großen Beliebtheit dieser Techniken kann man folgern, dass Quanten Computer auch bei der Simulation von Zufallszahlen und Berechnungen von Erwartungswerten eine Rolle spielen werden.

Die Hürden dieser Verfahren liegen in dem State Preparation, dem Vorgang, einen gewollten Quantenzustand mit hoher Präzision zu erzeugen. Während auch andere Methoden existieren, wollten wir ein einfaches konstruktives Beispiel zeigen. Für ein kleines Spielzeugbeispiel sind bereits heutige 5 Qubit Prozessoren von IBM fähig, das vorhergesagte Verhalten aufzuzeigen. Jedoch muss eine Analyse interessanter Anwendungsfälle aus der Industrie, Wirtschaft und Forschung nun eine Aufgabe zukünftiger Forschung sein.

Der Wunsch dieses Berichts war es, diese Tatsache etwas zu beleuchten und somit insbesondere der Wirtschaft einen verständlichen Zugang zu diesem Quantenvorteil zu ermöglichen. Bereits heute sehen wir Ergebnisse, wie sie in den Arbeiten [7,8,13] dargelegt werden, als zeitnahe Anwendung der frühen Quantenprozessoren. Es sei jedoch auch gesagt, dass es noch ein paar Jahre braucht, die angeführten Techniken in einem Umfang berechnen zu können, so dass „klassische“ Computer nicht mehr mithalten können. Wie in allen sich schnell ändernden High-Tech Bereichen ist die Entwicklung auch für Experten schwer vorherzusagen.

Danksagung

Wir wollen uns bei \philipp Leser & Daniel K. Park für die viele wertvollen Diskussionen zu diesem Thema bedanken.

In dieser Arbeit werden Ergebnisse zitiert und gezeigt, die mit dem IBM Q erstellt wurden. Die Aussagen in dieser und zitierten Arbeiten sind die der Autoren und nicht der offiziellen Position der IBM oder des IBM Q Teams.

Referenzen

[1]Chakrabarti, S. et al. A Threshold for Quantum Advantage in Derivative Pricing. Arxiv (2020).

[2]Fowler, A. G. & Gidney, C. Low overhead quantum computation using lattice surgery. Arxiv (2018).

[3]Preskill, J. Quantum Computing in the NISQ era and beyond. Quantum 2, 79 (2018).

[4]Montanaro, A. Quantum speedup of Monte Carlo methods. Proc Royal Soc Math Phys Eng Sci 471, 20150301 (2015).

[5]Rebentrost, P., Gupt, B. & Bromley, T. R. Quantum computational finance: Monte Carlo pricing of financial derivatives. Phys Rev A 98, 022321 (2018).

[6]Rebentrost, P. & Lloyd, S. Quantum computational finance: quantum algorithm for portfolio optimization. Arxiv (2018).

[7]Blank, C., Park, D. K. & Petruccione, F. Quantum-enhanced analysis of discrete stochastic processes. Arxiv (2020).

[8]Woerner, S. & Egger, D. J. Quantum Risk Analysis. Npj Quantum Information 5, 15 (2019).

[9]Shor, P. W. Polynomial-Time Algorithms for \prime Factorization and Discrete Logarithms on a Quantum Computer. Siam J Comput 26, 1484–1509 (1997).

[10]Shor, P. W. Algorithms for quantum computation: discrete logarithms and factoring. Proc 35th Annu Symposium Found Comput Sci 124–134 (1994) doi:10.1109/sfcs.1994.365700.

[11]Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information. (2009) doi:10.1017/cbo9780511976667.

[12]Brassard, G., Hoyer, P., Mosca, M. & Tapp, A. Quantum Amplitude Amplification and Estimation. Arxiv (2000).

[13]Stamatopoulos, N. et al. Option Pricing using Quantum Computers. Quantum 4, 291 (2020).

[14]Egger, D. J., Gutiérrez, R. G., Mestre, J. C. & Woerner, S. Credit Risk Analysis using Quantum Computers. Arxiv (2019).

[15]Park, D. K., Sinayskiy, I., Fingerhuth, M., Petruccione, F. & Rhee, J.-K. K. Parallel quantum trajectories via forking for sampling without redundancy. New J Phys 21, 083024 (2019).

[16]Iten, R., Colbeck, R., Kukuljan, I., Home, J. & Christandl, M. Quantum circuits for isometries. Phys Rev A 93, 032318 (2016).

[17]Malvetti, E., Iten, R. & Colbeck, R. Quantum Circuits for Sparse Isometries. Arxiv (2020).

[18]Shende, V. V., Bullock, S. S. & Markov, I. L. Synthesis of quantum-logic circuits. Ieee T Comput Aid D 25, 1000–1010 (2006).

[19]Plesch, M. & Brukner, Č. Quantum-state preparation with universal gate decompositions. Phys Rev A 83, 032302 (2011).

[20]Mottonen, M., Vartiainen, J. J., Bergholm, V. & Salomaa, M. M. Transformation of Quantum States Using Uniformly Controlled Rotations. Arxiv 5, 467–473 (2005).

[21]Peruzzo, A. et al. A variational eigenvalue solver on a photonic quantum processor. Nat Commun 5, 4213 (2014).

[22]Romero, J. & Aspuru-Guzik, A. Variational quantum generators: Generative adversarial quantum machine learning for continuous distributions. Arxiv (2019).

[23]Wecker, D., Hastings, M. B. & Troyer, M. Progress towards practical quantum variational algorithms. Phys Rev A 92, 042303 (2015).

[24]Chowdhury, A. N., Low, G. H. & Wiebe, N. A Variational Quantum Algorithm for Preparing Quantum Gibbs States. Arxiv (2020).

[25]Zoufal, C., Lucchi, A. & Woerner, S. Quantum Generative Adversarial Networks for learning and loading random distributions. Npj Quantum Information 5, 103 (2019).

[26]Araujo, I. F., Park, D. K., Petruccione, F. & Silva, A. J. da. A divide-and-conquer algorithm for quantum state preparation. Arxiv (2020).

[27]Enriquez, N. A simple construction of the \fractional Brownian motion. Stoch Proc Appl 109, 203–223 (2004).