Quantentechnologien entwickeln sich sehr dynamisch. Forschungsinstitute und Universitäten, aber auch Firmen treiben die Entwicklung. Folglich entstehen verschiedene Modelle mit eigenen Vor- und Nachteile, deren Praxisreife ganz unterschiedlich ist. Welches sind die wichtigsten Anwendungsfelder, in denen Quantentechnologie großen Einfluss haben wird? Wie weit sind die einzelnen Konzepte und welche können schon heute wirtschaftlich eingesetzt werden?
In den vergangenen Jahren galt das Label „Künstliche Intelligenz“ vielen als Synonym für moderne, schnelle und überlegene technologische Lösungen. Eine ähnliche Situation erleben wir im Moment mit Quantentechnologien. Die vielfältigen Entwicklungen im Bereich der Systeme, Anwendungen und Services, die aus Quantentechnologien hervorgegangen oder von ihnen inspiriert worden sind, sind bereits für einige praktische Anwendungsfälle relevant. Doch eben nur für einige. Auch das Etikett „Quanten“ bedeutet bei weitem nicht immer dasselbe: Simulator, Emulator, adiabatisches System, Ionenfalle sind nur einige der Begriffe, die in diesem Zusammenhang genannt werden.

Die Erprobung bzw. der Einsatz von Quantentechnologien sollte daher immer gemeinsam mit z. B. der geschäftlichen Fragestellung betrachtet und entschieden werden. Aber für welche Fragestellungen eignen sich Quantencomputer und was ist eigentlich der Unterschied zwischen einem Quanten Gate Computer mit 49 Qubits, einem adiabatischen Quantencomputer, einem One-Way Quantencomputer, einem Quanten Annealer mit mehr als 2.000 Qubits und Simulated Annealing oder Digital Annealing?

Fragestellungen für Quantentechnologien

Theoretisch können mit Hilfe von Quantentechnologie alle Probleme bearbeitet bzw. gelöst werden, die auch auf herkömmlichen Computern, also deterministischen Turing-Maschinen, berechnet werden können. Auf Grund der technisch jedoch sehr komplizierten Umsetzung, der Berücksichtigung der Nachteile von quantenmechanischen Effekten bei wohldefinierten Operationen und der Tatsache, dass eine neuartige Programmierung entwickelt werden muss, liegt das Hauptaugenmerk der Forschung vor allem auf den Bereichen, in denen heutige Rechnerarchitekturen nicht praktikable Laufzeiten oder sehr viel Speicherplatz benötigen würden. Somit stehen momentan vier im Mittelpunkt:

• (energetische) Optimierungsaufgaben (z. B. Metropolis-Hastings-Algorithmus)
• Kryptografische Verfahren (z. B. der Shor-Algorithmus)
• Suche in sehr großen Datenmengen (z. B. der Grover-Algorithmus)
• Quantum Artificial Intelligence

Insbesondere die näherungsweise bzw. (ausreichend) gute Lösung von Optimierungsaufgaben ist eines der Gebiete, auf dem schon seit den 50er Jahren geforscht wird und das daher gut verstanden ist. Dies und die Tatsache, dass ein Qubit theoretisch unendlich viele Zustände darstellen kann, sind auch der Grund dafür, dass den Quanten Approximation Optimierungsalgorithmen (QAOA) aktuell die besten Chancen eingeräumt werden, die sogenannte Quantenüberlegenheit (engl. Quantum Supremacy) zu beweisen (ob dies nicht schon geschehen ist und die wissenschaftliche Diskussion dazu sollen in diesem Artikel nicht Thema sein).

Optimierung und der Metropolis-Hastings-Algorithmus

Kombinatorische Optimierung ist der Prozess, eine oder mehrere optimale Lösungen eines Problems zu finden. Gesucht werden diese Lösungen in einem diskreten (endlichen), aber sehr großen Konfigurationsraum (also einer Menge von Zuständen). Die Menge der möglichen Lösungen kann jeweils mit mehreren Bedingungen definiert sein und das Ziel ist es, mit der besten Lösung die Zielfunktion zu optimieren, also z. B. die Kosten zu minimieren oder den Gewinn zu maximieren. Da die Problemräume in bestimmten, sehr schweren Fragestellungen sehr groß sind, ist es extrem schwierig oder manchmal sogar unmöglich, optimale oder sogar eine einzige gute Lösung dieser Probleme mit klassischen Computern in angemessener Zeit oder Genauigkeit zu finden.

Für Unternehmen im privaten Sektor und auch für die öffentliche Hand stellen kombinatorische Optimierungsprobleme oftmals eine große Herausforderung dar, da diese Fragestellungen nicht oder nicht performant genug beantworten werden können. Die Aufgabenstellungen sind dabei oftmals einfach zu beschreiben, stellen sich aber schnell als sehr schwer zu lösen heraus. Kombinatorische Optimierungsprobleme lassen sich in Reihenfolge-, Zuordnungs-, Gruppierungs- und Auswahlprobleme aufgliedern und innerhalb dieser Klassen findet man dann Unterklassen, wie z.B. das Knapsack-Problem, das Traveling-Salesman-Problem (TSP), Boolesche Erfüllbarkeit (SAT), das Constraint Satisfaction Problem (CSP), Maximum Cut (MAX-CUT), Graphen-Ähnlichkeit, Portfolio-Optimierung, Routenoptimierung, (Termin)-Planung, (Aufgaben)-Zuweisung, Software-Validierung usw. Alle Probleme, die in diesen Klassen enthalten sind, haben die Eigenschaft, dass es für ihre Beantwortung, nicht nur eine, sondern durchaus extrem viele, qualitativ unterschiedliche Lösungen geben kann. Ganz wesentlich ist auch noch die Eigenschaft, dass kein bekannter Algorithmus existiert, der diese Probleme einfach direkt ausrechnen kann. Das Durchsuchen der sehr großen Problemräume nimmt also enorm viel Rechenkapazität und –zeit in Anspruch.

Anhand eines Beispiels wollen wir uns einmal ansehen, wie groß Such- oder Problemräume werden können. Ausgangsszenario ist ein Fußballstadion. In diesem Stadion existiert ein Block mit 500 Sitzplätzen. Es sollen jeweils 20 Fan-Gruppen, die z.B. aus bis zu 5 Personen bestehen dürfen, auf die 500 Sitze verteilt werden, so dass die Personen jeder Gruppe benachbart sitzen können und es muss ein Mindestabstand zwischen den Gruppen herrschen. Auch sollen bestimmte Sitzmuster für die Gruppen zugelassen sein. Die Aufgabe ist erst einmal einfach zu verstehen und man würde sich ohne technische Hilfsmittel wahrscheinlich im Tetris-Verfahren ans Ausprobieren von allen möglichen Kombinationen machen. Wie wir oben festgestellt haben, gehört auch diese Aufgabe, als Zuordnungsproblem mit dem Ziel Sitzplätze zu optimieren, zu einer Klasse von Problemen, die sehr schwer zu lösen sind. Es ist also tatsächlich notwendig, in dem benannten endlichen Suchraum Lösungen durch geschicktes Suchen zu finden. Der Versuch eine Lösung nach der anderen durch sequentielles Ausprobieren zu finden, kann im Übrigen relativ viel Zeit in Anspruch nehmen, da wir in diesem Beispiel tatsächlich von über 10³⁰⁰⁰ möglichen Kombinationen[1] sprechen. Das Finden von guten und gewünschten Lösungen gewinnt auch deshalb an Komplexität, da das Nichteinhalten der gewünschten Sitzmuster zwar den Suchraum nicht vergrößert, allerdings durch Strafterme die Berechnung umfangreicher machen. Es ist zu erwarten, dass ein Standard-Computersystem signifikant länger rechnen, um alle möglichen Kombinationen auf gültige Lösungen zu testen. Man stelle sich also vor, was es bedeutet, eine Verteilung von unterschiedlichen Gruppen auf ein gesamtes Stadion mit mehr als 50.000 Plätzen optimal und unter Einhaltung von speziellen Regeln, wie z. B. dem Mindestabstand durchzuführen. Dies führt v.a. bei Echtzeit-Anforderungen regelmäßig zu Herausforderungen für Standardverfahren, da in unserem Beispiel die Verteilung der Gruppen auf das gesamte Stadion eben nicht während der online-Buchung oder kurz danach durchgeführt werden kann.

Bereits 1953 publizierten Nicholas Metropolis et al. zur Lösung solcher Probleme einen Algorithmus, der 1970 von W. Keith Hastings generalisiert wurde. Der Metropolis-Hastings-Algorithmus stellt Optimierungsprobleme als Energielandschaft bzw. Energiefunktion dar. In dieser Funktion wird dann eine schrittweise Abkühlung des Systems simuliert, ähnlich wie die langsame Abkühlung eines Metalls oder Glases, mit der erreicht werden soll, dass die Atome bzw. Moleküle sich optimal – also einem Energieminimum entsprechend – anordnen (wodurch oft eine besonders hohe Festigkeit oder Langlebigkeit erreicht wird). Für bestimmte Formen der „simulierten Abkühlung“ (engl. Simulated Annealing) konnte bewiesen werden, dass sie das globale Minimum der vorher definierten Energielandschaft finden. In unzähligen anderen Fällen zeigt die praktische Erprobung, dass ein sehr gutes lokales Minimum gefunden wird.

Auch wenn der Metropolis-Hastings-Algorithmus nicht immer der effizienteste Weg ist, um ein Optimierungsproblem lösen, ist es ein genereller Weg. Aber eben auch einer, der auf herkömmlichen Rechenarchitekturen weiterhin sehr zeitintensiv ist. Dennoch sollten wir uns den Begriff des „Annealing“ merken, wir werden gleich wieder auf ihn stoßen. [i] [ii]

Quantencomputer ist nicht gleich Quantencomputer

Viele Firmen und deren Wissenschaftler verkünden in regelmäßigen Abständen neue Durchbrüche bei Quantencomputern. Die in den Pressemitteilungen genannte Anzahl der Qubits und die verschiedenen Umsetzungen können jedoch schnell für Verwirrung sorgen.

Ein „echter“ Quantencomputer ist ein System, das tatsächlich mit Quanten-Bits, also quantenmechanischen Zuständen arbeitet. Alleine hier gibt es aber bereits grundlegend verschiedene Konzepte: ein universeller Quantencomputer, auch als Quanten Gate Computer bezeichnet, ist das am schwierigsten umzusetzende Konzept. Er basiert darauf, dass die Quantenregister beliebig durch physikalische Operationen, sogenannte Quanten-Gatter, manipuliert werden können (das können z.B. Laserstrahlen, magnetische Einstrahlungen o. ä. sein). Das würde in etwa dem entsprechen, was wir heute auch als „normalen“ Computer bezeichnen – nur eben viel schneller. Quantum Gate Computer sind aktuell mit maximal 72 Qubits ausgestattet. [iii]

Daneben gibt es das Konzept der Einweg-Quantencomputer (engl. One-Way quantum computer). Bei diesen wird zunächst ein vom Problem unabhängiger Quantenzustand erzeugt und die eigentliche Berechnung erfolgt durch gezielte Messungen an diesem Zustand. Die Messungen beeinflussen ihrerseits den Zustand des Systems und bestimmen außerdem, wo als nächstes gemessen wird.

Das dritte – und im Gegensatz zum Einweg-Quantencomputer deutlich verbreitetere Konzept – ist der adiabatische Quantencomputer. Hier werden vereinfacht gesprochen zwei Quantenzustände erzeugt: der erste, komplizierte Quantenzustand, entspricht der Lösung des Problems, der zweite ist ein experimentell einfach herzustellender und wohldefinierter Zustand. Durch die schrittweise Überführung des zweiten in den ersten Zustand ist es möglich, die Lösung des komplizierten Problems zu finden. Diese Art von Quantenrechnern kann auf Grund ihrer Natur im wesentlichen kombinatorische Optimierungsprobleme lösen – ist aber technisch einfacher zu realisieren, da während des Messens bzw. davor und danach keine Manipulationen durch Quantengatter (engl. quantum gates) mehr erforderlich sind. Solche Quantenrechner gibt es seit September letzten Jahres mit mehr als 5.000 Qubits – wobei die volle Konnektivität der Qubits untereinander nicht gegeben ist.

Neben den verschiedenen Konzepten von Quantencomputern gibt es eine Vielzahl von verschiedenen physikalischen Implementierungen der Quanten bzw. Quantenzustände. Diese reichen von der Nutzung der Spins der Elektronen über die Energiewerte von Ionen bis zur Nutzung von Photonen oder supraleitenden Schaltkreisen mit Kreisströmen. [iv]

Annealing für Optimierungsaufgaben

Die Nutzung von Simulated Annealing auf Rechnern, basierend auf der von-Neumann Architektur, wurde bereits thematisiert und hat sich in den letzten Jahrzehnten in der Praxis bewährt. Wird statt eines klassischen Rechners nun ein adiabatischer Quantencomputer für die Lösung des Problems genutzt, dann spricht man vom „Quantum Annealing“. Das ermöglicht theoretisch eine deutlich schnellere Rechenzeit, bringt aber all die Nachteile von Quantenrechnern mit sich: technisch sehr anspruchsvolle Umsetzung und Umgebung, notwendige Fehlerkorrekturen der Lösung etc.

Eine intelligente Kombination des Simulated Annealing und den Prinzipien von Quanten Annealern stellen die Digital Annealer da. Sie basieren nicht auf der von-Neumann Architektur, sind aber dennoch „klassische“ Computerchips mit allen dementsprechenden Vorteilen wie geringe Größe oder, Standardanforderungen an Infrastruktur und Umgebung. Ähnlich wie beim Tunneling im Quantum Annealing erhöht der Digital Annealer die Ausbruchswahrscheinlichkeit aus einem lokalen Energiezustands-Minimum mit Hilfe dynamischer Energie, und erhöht die Konvergenzgeschwindigkeit mit Hilfe paralleler Zustandsauswertung. Daher ist er viel schneller, als traditionelle Simulated Annealing Techniken. Digital Annealing zeichnet sich außerdem durch stochastische Parallelität und volle Vernetzbarkeit der gegenwärtig 8.192 Hardware-Bits aus – Eigenschaften, die von den quantenmechanischen Phänomenen Superposition und Verschränkung inspiriert sind – wodurch das System in der Lage ist, große Probleme schnell und mit hoher Präzision zu lösen. Außerdem werden die Probleme auf die gleiche Weise formuliert, wie beim Simulated oder Quanten Annealing – als Energielandschaft. Mathematisch wird dies mit QUBOs realisiert. [v] [vi] [vii]

Was sind QUBOs?

QUBO steht für Quadratic Unconstrained Binary Optimization und ist eine Möglichkeit, Optimierungsprobleme als mathematische Formulierung (quadratisches Polynom mit einer endlichen Menge von binären Variablen) darzustellen. Weitere Darstellungen für Optimierungsprobleme sind z.B. HOBOs (Higher Order Binary Optimization) oder lineare Gleichungen (also nicht quadratische oder von höherer Potenz). Grundsätzlich ist die Formulierung über HOBOs vorteilhafter, da das Optimierungsproblem als Gleichung eleganter dargestellt werden kann. Gängige Solver, also Computerprogramme, die mathematische Probleme numerisch lösen, können aber in den meisten Fällen HOBOs nicht direkt verarbeiten, d.h. HOBOs müssen unter Einbindung zusätzlicher Variablen vorher in quadratische oder lineare Formulierungen umgewandelt werden. Aus diesem Grund wird die Darstellung über QUBOs oft bevorzugt und ermöglicht die Weiterverarbeitung von Optimierungsproblemen durch entsprechende Solver, wie z.B. Quanten Annealer, Digital Annealer oder im Simulated Annealing.

Optimierungsprobleme werden also über QUBOs in quadratischen Gleichungen dargestellt, wobei jeweils immer zwei Variablen miteinander korreliert werden. Zugelassen für die Optimierung sind grundsätzlich immer alle möglichen diskreten Zustände der Variablen. Mithilfe des Beispiels „Kombination von Kleidungsstücken“ soll der Aufbau eines QUBOs deutlich werden. Nehmen wir an, dass wir drei verschiedenfarbige Hemden (also z.B. rot, grün, blau) und drei verschiedenfarbige Hosen (ebenfalls rot, grün, blau) kombinieren wollen. Hemd und Hose in derselben Farbe passen immer optimal zueinander. Grundsätzlich ist es aber zulässig, alle Hemden und alle Hosen miteinander zu kombinieren. Zulässig ist auch, dass alle sechs Kleidungsstücke gleichzeitig angezogen werden. Diese Freiheit beschreibt das uneingeschränkte (= unconstrained) Verwenden der Variablen. Die binäre (= binary) Information an dieser Stelle beschreibt die beiden zulässigen Möglichkeiten ein Kleidungsstück entweder anzuziehen oder nicht anzuziehen. Nun ist es allerdings unvorteilhaft, wenn man mehr als ein Hemd oder eine Hose gleichzeitig anzieht oder Farben kombiniert, die nicht gut zusammenpassen. Daher führt man Bedingungen in Optimierungsgleichungen ein, die dies berücksichtigen. Diese Bedingungen werden als Strafterme formuliert, die das Ergebnis der Gleichung beeinflussen. Im Bekleidungsbeispiel bestraft man dann z.B. das gleichzeitige Tragen von mehr als einer Hose so hoch, dass die Optimierungsgleichung in diesem Fall im Ergebnis einen großen Wert bekommt. Damit fallen diese Kombinationen in der Gesamtschau aller möglichen guten oder optimalen Kombinationen heraus. Ein optimales Ergebnis einer Optimierungsgleichung ist nämlich eines mit einem möglichst geringen Wert (oder Energieminimum). Auch das Kombinieren von Hemd und Hose unterschiedlicher Farben in unserem Beispiel wird leicht bestraft und stellt damit zwar eine mögliche, aber keine gute Lösung dar. In kombinatorischen Optimierungsproblemen liegt also neben der mathematischen Darstellung der Optimierungsfunktion immer auch die Aufgabe in der Erweiterung der Gleichung durch Strafterme, die für eine entsprechende Gewichtung, abhängig von der Relevanz der Bedingung im geschäftlichen Kontext, sorgen. Gewichtet werden können dabei entweder einzelne Variablen oder die Kombination aus zwei Variablen (was den quadratischen Charakter des QUBOs ausmacht). Die Tatsache, dass in diesem Beispiel nur zwei Variablen (Hemd und Hose in entsprechenden Farben) gewählt wurden, dient nur der Vereinfachung. Es ist durchaus möglich mehrere Variablen miteinander zu korrelieren, wobei alle berücksichtigt, aber jeweils immer nur zwei Variablen kombiniert betrachtet und gewichtet werden.

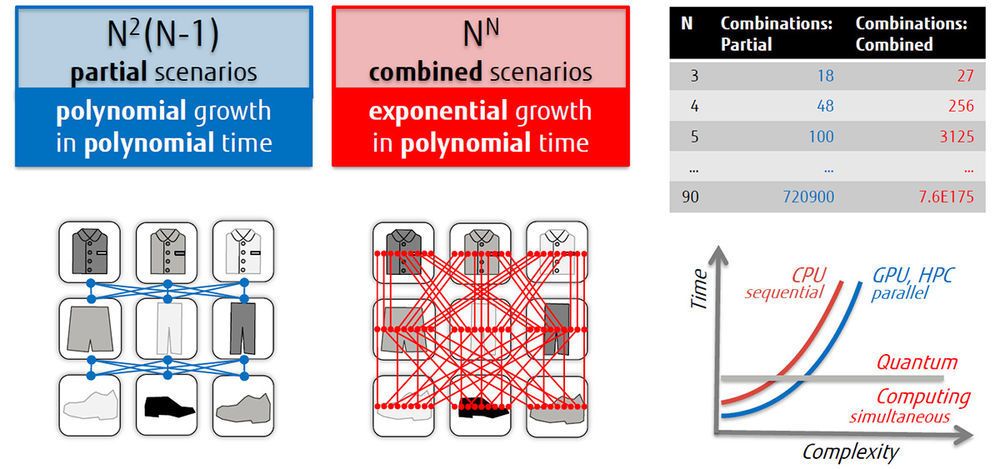
Vorstellen kann man sich die Kombination von Hemden und Hosen auch, in dem man z.B. die Hemden auf der y-Achse und die Hosen auf der x-Achse eines Koordinatensystems anbringt. An den jeweiligen Gitterpunkten entstehen dann die möglichen Kombinationen, die man dann jeweils mit Strafen belegen kann, wenn bestimmte Kombinationen nicht gewünscht sind. Tauscht man die Hemd-Hose Kombinationen durch Magnete aus, kommt man im Übrigen zu einem Versuchsaufbau, der auf Ernst Ising zurückgeht. Im Ising-Gittermodell sind in einem mehrdimensionalen Gitter Ferromagneten angeordnet, die sich aufgrund ihrer Eigenschaften gegenseitig beeinflussen und bezogen auf das Gesamtsystem einen Zustand suchen, der möglichst energiearm ist. Diese für die Magnete optimale (binäre) Ausrichtung (also nach Norden oder Süden) kann ebenfalls in einer Energiegleichung dargestellt werden, die identisch mit den oben beschriebenen QUBOs ist.

QUBOs stellen also eine sehr gute Möglichkeit dar, Optimierungsfragestellungen für Solver, wie z.B. Quanten Annealer oder Digitale Annealer bis hin zu neuromorphen Computersystemen zu formulieren. [viii] [ix] [x]

Anwendung in der Praxis: Portfolio-Optimierung

Die Anwendung von Quantentechnologie im Unternehmensumfeld ist heute im wesentlichen noch Zukunftsmusik, nicht jedoch die Nutzung ihrer Vorteile. Welche vielfältigen Probleme Digital Annealing bereits heute lösen kann, zeigen die folgenden Beispiele aus den verschiedensten Branchen. Den Anfang macht die Finanzbranche.

Bild: Portfolio Risk Optimization_Bsp Commerzbank AG_139.pdf
BU: Die Commerzbank-Einheit Incubator Main möchte mithilfe von Digital Annealing die Absicherung von Leasing-Verträgen optimieren. (Quelle: Fujitsu)

Die ideale Zusammenstellung eines Portfolios ist eine Wissenschaft, die in den Medien gut und gerne auch einmal esoterisch dargestellt wird. Wer sich damit beschäftigt hat, wie beispielsweise das eigene Aktienportfolio aussehen sollte, kann das sicher gut nachvollziehen. Dabei gibt es eine Reihe handfester Regeln und Fakten, die man zum Teil nur festlegen, zum Teil aber auch erst durch statistische Korrelationen oder anderweitige Kombinationen berechnen muss. Verbriefung nennt sich das Verfahren, bei dem ein Pool verschiedener finanzieller Vermögenswerte gestaltet wird. Das können Aktien, aber auch Leasing Verträge sein. Aus einem sehr großen Pool an vorhandenen Leasingaufträgen sollte hier eine Teilmenge ausgewählt werden, so dass ein bestimmtes Portfoliovolumen erreicht wird, während gleichzeitig eine Vielzahl von Faktoren berücksichtigt werden muss.

Diese Faktoren lassen sich grob in Parameter und Bedingungen unterteilen. Zu den Parametern gehören zunächst die mehreren Tausend Leasingobjekte selbst, aus denen ausgewählt werden muss. Jedes ist dabei mit einem Leasing-Volumen und einer Laufzeit ausgestattet, die berücksichtig werden müssen. Zu den Bedingungen, die ebenfalls in die Optimierung einfließen müssen, gehört zum Beispiel das maximale Volumen des Portfolios, die maximale Anzahl von erlaubten Short-Leasingobjekten – einer von vielen Faktoren zur Steuerung des Risikoprofils, das minimale Gesamtvolumen der Summe aller großen Leasingverträge, regulatorische Vorgaben und vieles mehr. All diese Informationen wurden im Rahmen der Quanten-inspirierten Optimierungsservices (QIOS) aufgenommen und kombinatorisch optimiert. In ersten Berechnungen zusammen mit dem Main Incubator GmbH konnte der Digital Annealer den Auswahlprozess beschleunigen und einen höheren Effizienzgrad erzielen, als mit derzeit im Einsatz befindlichen Ansätzen. [xi] [xii] [xiii] [xiv]

Optimierte Infrastruktur: Datenflüsse

Daten sind das neue Öl, oder Gold. Dieser nicht mehr ganz taufrische Vergleich aus den 2010er Jahren hat sich in beeindruckender Art und Weise in den Marktwerten der Elektronik- und Technologiekonzerne niedergeschlagen. Es kann nicht mehr geleugnet werden, dass Daten unsere Unternehmen und unsere Gesellschaft so stark wie nie zuvor antreiben. Zu einer gewinnbringenden Verarbeitung von Daten gehört aber auch immer ein performanter Transport derselben, und hier kommen die Telekommunikationsanbieter in Spiel, die sich gegenwärtig darum bemühen, noch mehr Daten noch schneller zu transportieren. Dieser Datenaustausch findet über Mobilfunknetze und festverbaute Leitungsinfrastruktur statt, die unsere Ballungszentren und auch ländlichen Gebiete wie ein Geflecht aus Nervenbahnen miteinander verbindet.

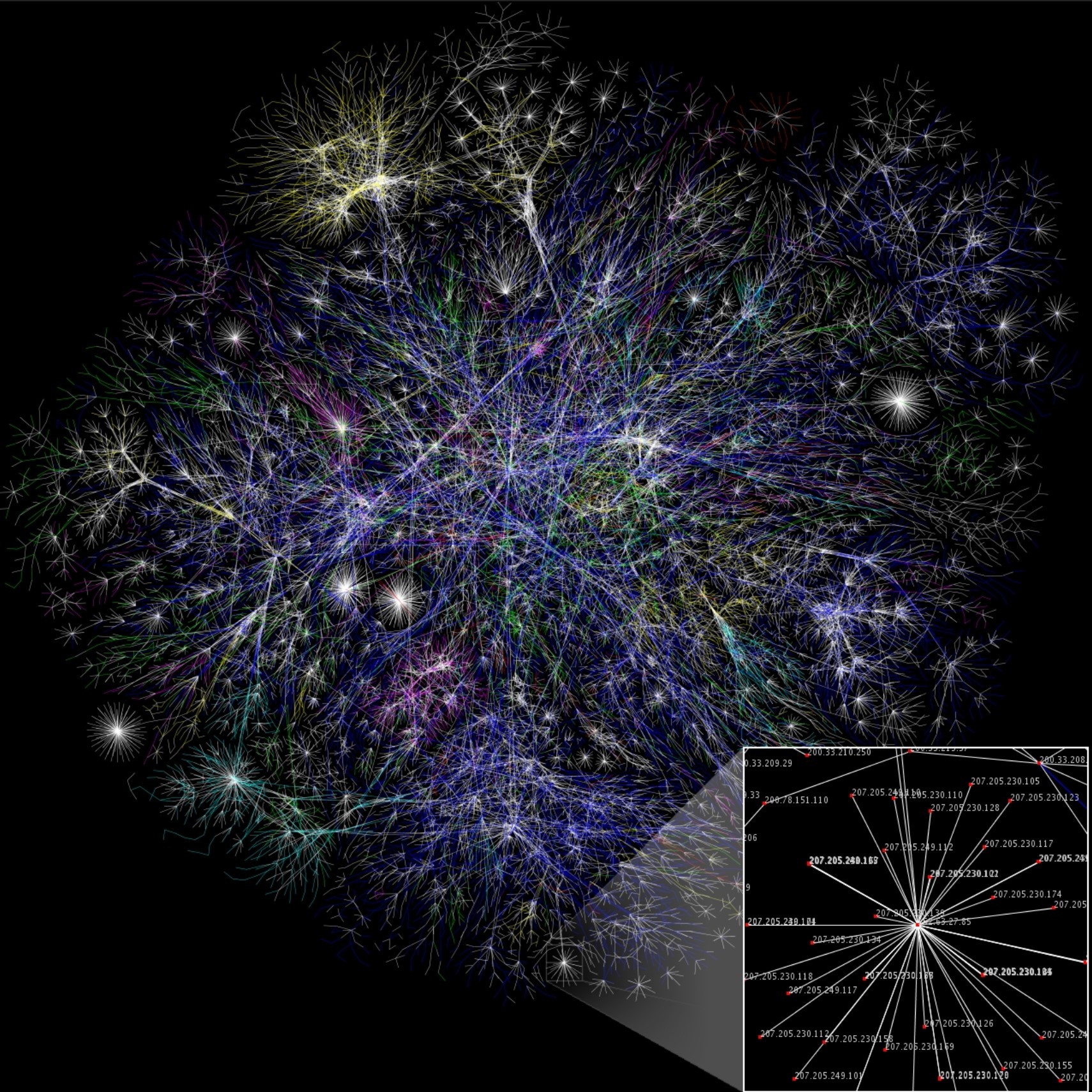
Alle Nutzer*innen der Leitungs- und Mobilinfrastruktur erwarten heutzutage einen performanten Zugriff auf Informationen, die auf der ganzen Welt verteilt in Rechenzentren liegen. Die grundsätzliche Erwartung an Telekommunikationsanbieter ist es, den bestmöglichen Up- und Download zu erhalten und das Schwankungen ggf. abgefedert werden. Die steigende Tendenz dezentral zu arbeiten (Stichwort: Homeoffice) und die aktuelle Einschränkung des Bewegungsradius der Bevölkerungen bringt dabei zusätzliche Dynamik in den Datentransfer. Vor allem kurzfristige ungeplante Events können jeweils zu kurzfristigen regionalen Auslastungs-Spitzen führen. Oder auch ganze Rechenzentren können, ebenso wie kleinere Netzelemente, ausfallen und damit bestimmte Netzsegmente aus dem Spiel nehmen. Für Telekommunikationsanbieter liegt also eine der Hauptaufgaben für eine performante Datenübertragung darin, kurz-, mittel- und langfristige Überlastungen von Netzsegmenten und Netzknoten auszugleichen. Es hat sich gezeigt, dass ein lokales Umleiten von Überlast das Gesamtsystem eher belastet und dafür an anderen Stellen Spitzen verursacht. Deshalb muss der Telekommunikationsprovider die Ziele aller Datenpakete in seinem Netzwerk im Auge behalten und jedem eine geeignete Route zuweisen, so dass alle Pakete gemeinsam ihr Ziel in der bestmöglichen Zeit erreichen. Das ist eine komplexe kombinatorische Aufgabe, die mit der heute verfügbaren Rechenleistung kaum zu lösen ist. Nur durch die Optimierung des Gesamtsystems, bestehend aus Knoten und Verbindungen, lässt sich eine nachhaltige Reduzierung der Last erreichen. Das konnte Fujitsu gemeinsam mit den T-Labs in einer Erprobung des Digital Annealers zeigen. [xv]

Die grüne Welle – Optimierung des Verkehrsflusses

Für den nächsten praktischen Anwendungsfall von kombinatorischer Optimierung begeben wir uns gedanklich in die deutsche Großstadt Hamburg. Die verantwortliche Behörde für den Hamburger Hafen, die Hamburg Port Authorities (HPA) haben eine Vision entwickelt: der Straßenverkehr im Hafengebiet soll optimiert werden.

Der Hamburger Hafen ist der drittgrößte europäische Hafen, auf dem pro Jahr 900 Millionen Containern umgeschlagen werden. Im Hinterland-Verkehr docken 200 Züge pro Tag an, um Güter, die von ca. 10.000 Schiffen pro Jahr bewegt werden, an- und abzutransportieren. Unzählige LKWs belasten täglich die Straßen vom und zum 72 m² großen Hafengelände. Die zunehmende Überlastung der betroffenen Straßen hat nicht nur Auswirkungen auf das Hafengelände selbst, sondern wirkt sich auch negativ auf die Luftqualität aus.

Als Hauptverursacher der ungenügenden Verkehrssteuerung wurden ineffiziente Ampelschaltungen ausgemacht, die den Grad der Überlastung maßgeblich beeinflussen. Diese Erkenntnis veranlasste die HPA dazu, ein Projekt zum Entwurf eines intelligenten Ampelphasenmanagements für das Hafengebiet zu starten. Dazu wurde die technische Infrastruktur des Verkehrssystems in den letzten Jahren kontinuierlich ausgebaut. Neben der Aufrüstung auf den OCIT-Standards (ein Standard für offene Schnittstellen in der Straßenverkehrstechnik) werden die Straßen mit einem dichten Netz von Schleifensensoren, Wärmebildkameras und Bluetooth-Sensoren ausgestattet. Zusätzlich zu den Anforderungsschleifen direkt an der Kreuzung installierte das Verkehrsmanagement eine Vielzahl von Zählschleifen im Straßennetz. Diese können zwischen Pkw und Lkw unterscheiden und erfassen Abbiegeströme spurgenau. So entsteht ein umfassendes Bild der Verkehrssituation auf den wichtigen Straßen des Hafennetzes.

Man könnte nun annehmen, dass Staus mit dieser komplexen Überwachung des Verkehrs praktisch nicht mehr möglich sind. Tatsächlich sieht die Wirklichkeit aber anders aus. Die Belastung der Straßen nimmt zu und der Stress-Level steigt. Dies liegt vor allem daran, dass die Koordination der Verkehrssteuerung in Echtzeit sehr schnell an die Grenzen der Kapazität von herkömmlichen Steuersystemen stößt. Wenn man insgesamt die Grünzeiten der Lichtsignalsteuerung optimieren will, müssen die Daten des gesamten Netzes zusammengeführt und leistungsfähig verarbeitet werden. Bis jetzt war die Verarbeitung der Verkehrsdaten in Echtzeit nur an einzelnen Kreuzungen möglich. Man stellte fest, dass nicht nur eine hohe Rechenleistung, sondern auch ein ganz neuer Ansatz zur Berechnung der nicht-parallelisierbaren kombinatorischen Optimierung notwendig war. Daher reichte es nicht aus, auf leistungsfähigeren GPUs in High Performance Computing Umgebungen zu rechnen, da diese die zugrundeliegende rechnerische Herausforderung NP-harter Probleme nicht in der benötigten Zeit lösen können. Mit QIOS und dem Digital Annealer steht der HPA nun die Möglichkeit zur komplexen Berechnungen einer hohen Anzahl möglicher Szenarien in wenigen Sekunden zur Verfügung. Das ermöglicht Operationen nahe Echtzeit.

Das Ziel des aktuellen Optimierungsprojektes mit Fujitsu ist es, in Echtzeit für die aktuelle Verkehrslage optimale Signalschaltungen für alle Lichtsignalanlagen im gesamten Verkehrsnetz auszuwählen, um die Verkehrsteilnehmer vorausschauend durch den Hafenverkehr zu leiten, zum Beispiel durch Priorisierung erkannter Lkw-Züge. Darüber hinaus ermöglicht ein Verkehrslagebild weitere Analysen, z. B. für Reisezeitberechnungen und Verlustzeitbilder. Das Projekt zielt darauf ab, die Kapazität des bestehenden Straßennetzes im Rahmen einer Gesamtnetzbetrachtung zu erhöhen. Das dient auch der Nachhaltigkeit, denn die CO₂ Emissionen resultieren im Straßenverkehr zu großen Teilen aus ungleichmäßiger Fahrweise. So sollen nicht nur die Stillstandzeiten mit laufendem Motor reduziert werden, sondern auch die Schadstoffemissionen durch unnötiges Beschleunigen und Bremsen (Kraftstoffverbrauch, Bremsbelag- und Reifenabrieb) im Netz verringert werden. Die Optimierung des Verkehrs geht also Hand in Hand mit dem Schutz der Umwelt. [xvi]

Entwicklung von Wirkstoffen und Medikamenten

Die Entwicklung von Wirkstoffen und Medikamenten ist oftmals ein langwieriger und sehr kostenintensiver Prozess. Das liegt insbesondere daran, dass eine Vielzahl von Stoffen nach dem Versuch-und-Irrtum Prinzip getestet werden müssen. Woran liegt das?

Um eine Krankheit zu bekämpfen, muss ein entsprechendes Medikament oder ein Wirkstoff mit dem Stoff oder Lebewesen (z. B. Bakterien) interagieren können, das die Krankheit auslöst oder aber mit den Zellen im menschlichen Körper, die bereits befallen worden sind. Diese Wechselwirkung basiert in vielen Fällen darauf, dass zwei Moleküle – eines auf jeder Seite der Interaktion – zueinander passen und miteinander reagieren. Denn ohne einen „ersten Kontakt“ können keine weiteren Prozesse in Gang gebracht werden. Nun bieten krankheitserregende Lebewesen oder erkrankte Zellen oft nicht nur eine Option für eine mögliche Andockstelle, sondern viele. Und wirksame Medikamente können sozusagen von überall kommen – von der Anwendung bereits bekannter Stoffe, über deren Abwandlung bis zur Nutzung vollkommen neuer Moleküle steht eine riesige Auswahl biologischer und chemischer Komponenten zur Verfügung. Natürlich werden bereits heute Einschränkungen vorgenommen. So orientieren sich Wissenschaftler*innen z. B. an Best Practices – welche Moleküle eines Krankheitserregers oder einer erkrankten Zelle eignen sich der Erfahrung nach besonders gut, um dort mit Medikamenten anzugreifen? Welche genauen Spezifikationen hat diese Kontaktstelle? Das können elektrische Ladungen, die physikalisch ausgebildete Form, die dort platzierten Aminosäuren und vieles mehr sein. Dazu wiederum suchen die Wissenschaftler*innen in einer Vielzahl an Datenbank die passenden, potenziellen Gegenstücke. Dennoch führt das in aller Regel zu einer viel zu großen Auswahl an Molekülen, die dann alle aufwendig im Labor getestet werden müssen.

Mit Hilfe des Digital Annealers konnte das Auffinden guter Kombinationen nicht nur deutlich beschleunigt, sondern auch noch mit einem Score versehen werden. Dazu wurden zunächst die Moleküle bzw. Proteine in einen Digitalen Zwilling umgewandelt, die später das Ziel des Medikaments werden sollten. Anschließend wurden die Nebenbedingungen mit Hilfe eines QUBOs formuliert. Um jedoch effizient eine optimale Kombination aus Faktoren (und damit den zugehörigen, potenziellen Wirkstoff zu finden), brauchte es eine Datenbank, in der die Werte der Funktionen der Nebenbedingungen für alle eingetragenen Wirkstoffe gespeichert waren. In einem Projekt mit dem Pharmakonzern POLARISqb musste diese erst zusammen mit Spezialisten von Fujitsu erstellt werden. Nach der Optimierung der Eingangsparameter dauerte die Suche für jeden QUBO weniger als eine Sekunde und der zeitgleich berechnete Score gab die Qualität des Ergebnisses in Bezug auf die Nebenbedingungen an. Damit konnte ein Prozess, der normalerweise mehr als ein Jahr dauert, insgesamt auf acht Wochen reduziert werden. [xvii] [xviii] [xix]

Quanten-Systeme und der Wert von Brückentechnologien

Wenn universelle Quantencomputer mit einer ausreichend großen Anzahl an Qubits für die reguläre Nutzung zur Verfügung stehen, werden sie die IT-Welt gehörig auf den Kopf stellen. Alleine die Konsequenzen für heute durch kryptografische Verfahren geschützte Daten und der Umgang damit sind nicht abzusehen. Aber bis es soweit ist, wird es noch eine Weile dauern. IBM hat zum Beispiel erst Ende 2020 angekündigt, dass sie mit der Implementierung ihres Quanten Gate Computers auf der Grundlage von supraleitenden Schaltkreisen mit 49 Qubits an Grenzen gestoßen sind, die sie mit dieser Technologie sehr wahrscheinlich nicht überwinden können. Sie setzen ihre Forschungsbemühungen daher in Richtung Silizium-Ionen fort und wollen mit der Quantelung derer Energieniveaus eine deutliche Miniaturisierung der Architektur und eine verbesserte Nutzung von Quanten-Gattern erreichen.[xx] Auch Photonen-basierte Implementierungen gewinnen an Zuspruch, liegen aber in der Forschung noch weit zurück. [xxi]

Für die Lösung einer Vielzahl an Aufgaben werden wir daher um die Nutzung von Brückentechnologien nicht herumkommen. Und das ist kein Manko, sondern eine Stärke. Quantencomputer sind erst einmal ein Stück Hardware – erst die Anwendung generiert den wahren Mehrwert. Und wie vorher dargelegt, muss dazu ein Problem in einem QUBO Ansatz formuliert werden. Brückentechnologien stellen daher nicht nur ein Bindeglied zu zukünftigen Quantencomputern dar, sondern bieten die Möglichkeit, relevante Problemstellungen bereits heute adressieren zu können.

Kooperationen mit Universitäten auf der ganzen Welt

Ebenso wie in den Jahrzehnten der Entwicklung der von-Neumann Architektur bestimmt auch bei der Entwicklung der Quantencomputer die Anzahl der verfügbaren Qubits die Größe der Probleme, die adressiert werden können. Bei herkömmlichen IT-Systemen steht beispielsweise die 64 Bit Architektur dafür, wie viele Bits der Rechner benutzt, wenn er Informationen im Speicher ablegt und wie groß die Registerbreite ist, die der Prozessor nutzen kann, um mathematische Berechnungen durchzuführen. Eine 64 Bit Maschine kann also 2⁶⁴ Werte darstellen, während eine 32 Bit Maschine nur 2³² Werte in einem Register darstellen kann. Das ist auch relevant, wenn es um die Menge des adressierbaren Speichers geht. Da ein Qubit theoretisch unendlich viele Zustände annehmen kann, hinkt der Vergleich natürlich. Dennoch kann man sich gut vorstellen, dass jedes Qubit einer Entität bzw. einem Objekt entspricht. Für das Kleidungsbeispiel aus dem Abschnitt über die QUBOs würden wir also drei Qubits für die Hemden und drei Qubits für die Hosen benötigen. So wird sehr deutlich, wie weit der Weg noch ist, den Quantencomputer in ihrer Entwicklung gehen müssen. Und auch der Digital Annealer stößt mit seinen aktuell 8.192 Hardware-Bits an Grenzen. Aus diesem Grund arbeiten die Fujitsu Laboratories Ltd. in Japan beständig daran, diese zu erhöhen. In ersten Laborversuchen ist es bereits gelungen, die Lösung von Problemen mit 1.000.000 benötigten Entitäten zu berechnen.

Um dieses Ziel zu erreichen haben die Fujitsu Laboratories mit dem Digital Annealer unter Anwendung einer neuen parallelen Suchtechnologie die weltweit erste praktische Lösung im Maßstab von einem Megabit für eine Ising-Maschine erfolgreich demonstriert. [xxii]

Aber nicht nur die Weiterentwicklung der Brückentechnologien ist ein wichtiges Thema. Im März 2020 wurde die Zusammenarbeit mit dem Start-Up Quantum Benchmark, dass von führenden Wissenschaftler*innen des Institute for Quantum Computing der University of Waterloo gegründet wurde beschlossen, um die Entwicklung von Methoden zur Fehlerkorrektur in Quantencomputern voran zu treiben. Darüber hinaus gibt es auch einen regen Austausch über die Entwicklung von Quantenalgorithmen, die insbesondere in den Bereichen Pharmazie- und Materialforschung für Verbesserungen sorgen können. [xxiii]

Im Oktober letzten Jahres verkündeten Fujitsu und Dataport die gemeinsame Unterstützung eines Lehrstuhls für Kombinatorische Optimierung in der Industrie an der Technischen Universität in Hamburg. Die Stiftungsprofessur ist auf zehn Jahre ausgelegt. Damit soll die Grundlagenforschung auf diesem wichtigen Einsatzgebiet weiter vorangetrieben werden und gleichzeitig ein Beitrag zur Ausbildung neuer Talente für Wissenschaft und digitale Wirtschaft geleistet werden. [xxiv]

Ebenso im Oktober wurden die Kooperationen mit RIKEN und der University of Tokyo, mit der TU Delft in den Niederlanden und der Osaka University angekündigt. Im ersten Projekt geht es insbesondere um die Einbindung von Quanten- und Quanten-inspirierten Technologien in große Rechenzentren, so dass eine reibungslose und sich ergänzende Zusammenarbeit beider Architekturen möglich ist. Gemeinsam mit der TU Delft wird an der Entwicklung von Diamanten-basierten Spin Qubits gearbeitet. In diesen aus Farbdefekten bestehenden Qubits können gleich mehrere verschiedene Spins (Elektronspin, Kernspin) für verschiedene Aufgaben genutzt werden. Der Elektronspin lässt sich schnell manipulieren und eignet sich gut um Quantenoperationen durchzuführen. Die Kernspins besitzen extrem langlebige Quantenzustände, bis hin zu 70s, und sind deshalb vielversprechende Kandidaten für Quantenspeicher. Die Zusammenarbeit mit der Osaka University bezieht sich vor allem auf die Entwicklung von Quantenalgorithmen und Methoden zur Fehlerkorrektur. [xxv]

Quantenalgorithmen – Ausblick

Dass die Anzahl der verfügbaren Qubits erhöht werden muss, steht außer Frage. Doch wann es soweit sein wird, ist ungewiss, ebenso wie die Frage, wie Quantencomputer dann in der Praxis genutzt werden können. Und auch die Steigerung der verfügbaren Hardware-Bits des Digital Annealer genügt nicht für alle Probleme. Daher wird natürlich auch stetig an den Algorithmen und Datenstrukturen geforscht, wie die oben beschriebenen Kooperationen zeigen. Zu den aktuellen Entwicklungen aus diesem Bereich ein kurzer Ausblick.

Feature Selection – Die Feature Selection ist ein Verfahren, bei dem im Vorfeld die Datenmenge bzw. die Anzahl ihrer Eigenschaften reduziert werden soll, damit der eigentliche Trainingsalgorithmus weniger Zeit benötigt. Das grundlegende Verfahren dahinter wird in der statistischen Analyse schon länger angewendet: die Eigenschaften der Daten werden auf Korrelationen untereinander hin untersucht. Werden zwei oder mehr Eigenheiten identifiziert, die eine starke Korrelation zueinander aufweisen, kann man diese entweder durch Zusammenführung und der Auswahl eines und Eliminierung der anderen Eigenschaften verringern. Stellt man die Frage nun anders herum, erhält man geschickter Weise wieder ein Optimierungsproblem: Welche Auswahl an Features bzw. Eigenschaften beschreibt die vorhandenen Daten optimal? Hierzu kann ein QUBO entworfen werden, der die entsprechende Feature Selection vornimmt. Der Prozess hat zwei weitere Vorteile: Normalerweise erfordert die Auswahl von relevanten Eigenschaften immer mindestens eine*n Domänenexpert*in, der aus der Erfahrung heraus eine Grundmenge vorgibt und beim Auswahlprozess unterstützt. Das ist aber nicht immer möglich und in diesem Fall auch nicht notwendig, da die Auswahl direkt an Hand der Daten erfolgt und zwar so, dass die Features möglichst unabhängig voneinander und aussagekräftig sind. Zum zweiten kann so einer potenziellen Zerlegung von Problemen, die normalerweise zu groß sind, um sie auf aktueller Hardware zu lösen, zuvorgekommen werden. [xxvi]

QBoost – Boosting ist ein adaptives Verfahren welches viele („tausende“) „einfache“ bzw. schwache Klassifizierer bewertet und hieraus einen sehr guten oder starken Klassifizierer baut. Hierbei wird die Bewertung der Klassifizierer über einen QUBO spezifischen Ansatz realisiert. Der Quanten Ansatz versetzt hierbei den QBoost Algorithmus in die Lage, alle vorgegebenen schwachen Klassifizierer gleichzeitig zu bewerten sowie auch in einem passenden Ensemble zusammenzustellen. [xxvii]

Quantum Machine Learning

Maschinelles Lernen (ML) stellt eine potenziell interessante Anwendung für Quantencomputing dar. Aktuelle klassische Ansätze für ML benötigen riesige Rechenressourcen und in vielen Fällen kostet das Training sehr viel Zeit. Quantencomputer versprechen nicht nur eine mehrfache Beschleunigung des Modelltrainings, sondern erlauben es auch, noch größere Datenmengen einzubeziehen, die für ein gut trainiertes Modell erforderlich sind. Von Quantencomputer ist Folgendes zu erwarten:

• Schnellere Laufzeiten für das Training von ML-Modellen
• Erhöhte Lernkapazität, da sie in der Lage sind, aus riesigen Datenmengen zu lernen

Die beiden oben genannten Aspekte werden in Kombination bessere und effizientere ML-Modelle ermöglichen. [xxviii]

Ein Beispiel zu Quantenneuronalen Netzen: Ein Datensatz mit etwa 10.000 Merkmalen benötigt auf einem klassischen Computer 10.000 Bits. Auf einem universellen Quantencomputer kann der gleiche Datensatz auf nur 14 Qubits abgebildet werden. Steigt die Anzahl der Features, sagen wir auf 10 Millionen, bleibt die Anzahl der benötigten Qubits bei nur 25. Auf einer klassischen Hardware führt das Einlesen von Datensätzen, ohne jegliche Reduktion der Dimensionen schnell zu einem Speicherüberlauf. Bei QNN sieht man deutlich eine logarithmische Effizienz für den Speicherplatzbedarf der Trainingsdaten. Was die Abbildung von Fließkommazahlen betrifft, so gibt es bereits polynomielle Unterprogramme, um die Fließkommazahlen auf die Quantenzustandsamplitude der beteiligten Qubits abzubilden.

Ein weiterer rechenintensiver Schritt beim Training eines neuronalen Netzwerks ist der Backpropagation-Schritt, der im Grunde genommen den Gradienten in Bezug auf alle Gewichte berechnet, für den Gradientenabstiegs-Optimierungsalgorithmus. Der Gradientenabstiegsalgorithmus ist an sich ein sehr schneller Algorithmus für die Optimierung von kontinuierlichen Funktionen. Bei neuronalen Netzwerken ist die Optimierungsfunktion jedoch eine multivariate Funktion mit Millionen bis Milliarden von zu optimierenden Parametern. Klassischerweise wird der Gradient mithilfe des Backpropagation-Algorithmus berechnet. Auf einem Quantencomputer können die Gradienten berechnet werden, indem man zwei Vorwärtsdurchläufe durchführt, einen auf die betreffende Variable und den zweiten Durchlauf mit einem kleinen Offset zum Variablenwert. Die Erwartungswerte, die sich aus den beiden Durchläufen ergeben, können dann verwendet werden, um den Gradienten in Bezug auf die Variable zu berechnen. [xxix]

Über dieses Beispiel hinaus gibt es mehrere Gattermodell-Algorithmen wie Grovers Algorithmus, den HHL Algorithmus usw., die als unterstützende Subroutinen für Quantum Machine Learning Modelle dienen können. Der Vorteil von Quantencomputern für verschiedene Modelle des maschinellen Lernens wurde bereits für einige der bekanntesten ML-Algorithmen theoretisch bewiesen, z. B. für Neuronale Netze, Support Vector Machines (SVM), Principle Component Analysis (PCA), Reinforcement Learning, Bayes’sche Inferenz und Boltzmann-Maschinen. [xxx]

Seit Anfang 2020 ist Fujitsu assoziierter Partner des Projektes PlanQK. Ziel der vom Bundesministerium für Wirtschaft und Energie geförderten Initiative ist die Entwicklung einer Plattform und eines Ökosystems für Quantenunterstützte Künstliche Intelligenz. Nutzer*innen, Entwickler*innen und Spezialisten soll so gleichermaßen einen leichten Zugriff auf Ressourcen und Konzepte zu ermöglichen. Das unterstützen wir gerne und blicken mit Spannung auf die aktuellen Entwicklungen. [xxxi]

Die Autoren möchten sich ganz herzlich für Zulieferungen, Anregungen und Hilfestellungen bei Dr. Abhishek, Dr. Sebastian Engel, Dr. Christian Münch, Andreas Rohnfelder, Isabel Schwende und Dr. Stefan Walter bedanken.

Quellen und Referenzen:

[i] Metropolis, Nicholas; Rosenbluth, Arianna W.; Rosenbluth, Marshall N.; Teller, Augusta H.; Teller, Edward (1953). „Equation of State Calculations by Fast Computing Machines“. The Journal of Chemical Physics. 21 (6): 1087. Bibcode:1953JChPh..21.1087M. doi:10.1063/1.1699114.

[ii] A. Das and B. K. Chakrabarti (Eds.), Quantum Annealing and Related Optimization Methods, Lecture Note in Physics, Vol. 679, Springer, Heidelberg (2005).

[iii] https://ai.googleblog.com/2018/03/a-preview-of-bristlecone-googles-new.html

[iv] Quantencomputer – Wikipedia

[v]  Kirkpatrick, S.; Gelatt Jr, C. D.; Vecchi, M. P. (1983). „Optimization by Simulated Annealing“. Science. 220 (4598): 671–680. Bibcode:1983Sci…220..671K. CiteSeerX 10.1.1.123.7607. doi:10.1126/science.220.4598.671. JSTOR 1690046. PMID 17813860. S2CID 205939.

[vi] Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1979). „Statistical-Thermodynamic Approach to Determination of Structure Amplitude Phases“. Sov.Phys. Crystallography. 24 (5): 519–524.

[vii] Khachaturyan, A.; Semenovskaya, S.; Vainshtein, B. (1981). „The Thermodynamic Approach to the Structure Analysis of Crystals“. Acta Crystallographica. 37 (A37): 742–754. Bibcode:1981AcCrA..37..742K. doi:10.1107/S0567739481001630.

[viii] Endre Boros, Peter L Hammer & Gabriel Tavares (April 2007). „Local search heuristics for Quadratic Unconstrained Binary Optimization (QUBO)“. Journal of Heuristics. Association for Computing Machinery. 13 (2): 99–132. doi:10.1007/s10732-007-9009-3. S2CID 32887708.

[ix] Di Wang & Robert Kleinberg (November 2009). „Analyzing quadratic unconstrained binary optimization problems via multicommodity flows“. Discrete Applied Mathematics. Elsevier. 157 (18): 3746–3753. doi:10.1016/j.dam.2009.07.009. PMC 2808708. PMID 20161596.

[x] Annealing and QUBO Tutorials: Services : Fujitsu Deutschland

[xi] main incubator nutzt Digital Annealing-Technologie zur Optimierung von Verbriefungstransaktionen – Fujitsu Deutschland

[xii] main incubator ist schon dabei: Digital Annealing – Fujitsu-Interview (it-finanzmagazin.de)

[xiii] Helping Main Incubator with Digital Annealer – YouTube (Kann gerne bei Online-VÖ als Video eingebunden werden)

[xiv] Digitally transforming finance with Main Incubator – YouTube (Kann gerne bei Online-VÖ als Video eingebunden werden)

[xv] Mehr Internet für alle: T-Labs und Fujitsu optimieren die Nutzung der Netzinfrastruktur

[xvi] Wie kann der Hamburger Hafen als Blueprint für intelligente Städte dienen? – YouTube (Kann gerne bei Online-VÖ als Video eingebunden werden)

[xvii] POLARISqb and Fujitsu • POLARISqb

[xviii] Digital Annealer speeds up Polarisqb’s drug discovery platform 10,000 times faster than traditional molecular analysis – Fujitsu Global

[xix] Accelerating Drug Discovery : Fujitsu Global

[xx] IBM Research – Zurich, Quantum technology & computing

[xxi] Light-Based Quantum Computer Exceeds Fastest Classical Supercomputers – Scientific American

[xxii] Fujitsu Develops New Tech for Quantum-Inspired ‚Digital Annealer,‘ Achieving Megabit-class Performance (hpcwire.com)

[xxiii] Fujitsu Laboratories and Quantum Benchmark Begin Joint Research on Algorithms with Error Suppression for Quantum Computing (finanznachrichten.de)

[xxiv] Press Release: Fujitsu gibt der Kombinatorischen Optimierung in der Industrie einen akademischen Schub – mit einem neuen Lehrstuhl an der TU Hamburg (tuhh.de)

[xxv] Fujitsu Commences Joint Research with World-Leading Institutions for Innovations in Quantum Computing – Fujitsu Global

[xxvi] Andrew Milne, Maxwell Rounds, and Phil Goddard, Optimal feature selection in credit scoring and classification using a quantum annealer, White Paper 1Qbit.

[xxvii] Hartmut Neven, Vasil S. Denchev, Geordie Rose and William G. Macready, QBoost: Large Scale Classifier Training with Adiabatic Quantum Optimization, Workshop and Conference Proceedings 25:333–348, 2012 Asian Conference on Machine Learning.

[xxviii] Peters et al., Machine learning of high dimensional data on a noisy quantum processor, Fermilab-Pub-20-624-QIS, arXiv: 2102.09581.

[xxix] Biamonte et al., Quantum Machine Learning, Nature 549, 195-202 (2017).

[xxx] Peters et al., Machine learning of high dimensional data on a noisy quantum processor, Fermilab-Pub-20-624-QIS, arXiv: 2102.09581.

[xxxi] Home – PlanQK