Introduction

Everyday computers can be used to solve numerous tasks which are often too difficult for humans to do quickly. Whether it is finding the shortest route between your home and your work or automatically finding the solutions to puzzles such as sudoku’s, computers can solve these problems faster and often better than humans can. On the other hand, there are problems that are easy for humans, but much harder for computers to do automatically, such as face identification or pattern recognition in images.

The state-of-the-art technique for solving these problems is machine learning. Different types of machine learning exist, most of them boiling down to supplying data to a computer, which then learns to produce a required outcome. The more data is given, the closer the outcome will be to the actual solution or the higher the probability will be that the correct solution is found.

Even though machine learning has solved numerous problems and improved approximate solutions of many others, it also has its limitations. Training machine learning models requires many data samples and models may require a long time to be trained or produce correct answers. Quantum computers may be able to improve the performance of machine learning algorithms by exploiting the power of quantum mechanics.

In this article we give a brief overview of machine learning techniques and explain how and where quantum machine learning is expected to deliver benefits. Next, we introduce quantum computing in general and the Quantum Inspire platform, an online quantum computing platform developed by QuTech in The Netherlands, in particular. After that, we show the results of implementing one of the quantum machine learning algorithms we propose in the second section. We tested a machine learning algorithm to classify and subsequently generate two by two-pixel images. The machine learning algorithm learned the probability distribution of the input and tried to replicate this in the generated images. This task is inherently difficult when the distribution of the input is unknown. We show how this algorithm was implemented on the Quantum Inspire platform and make a comparison with classical results.

Quantum Machine Learning

Machine learning is a potential interesting application for quantum computing. Current classical approaches ask huge computational resources and in many cases training costs a lot of time. In machine learning, the machine learns from experience, using data examples, without a user or programmer giving it explicit instructions; the machine builds its own logic. Looking at classical machine learning, one can distinguish various types:

• Supervised learning – here labeled data is used, e.g. for classification problems. This means that the data that is used for learning contains information about the class it belongs to.
• Unsupervised learning – here you use unlabeled data for, e.g., clustering problems. Here data points have to be assigned to a certain cluster of similar points, without prior information.
• Semi-supervised learning – here partially labeled data is available and models are investigated to improve classification using labeled data with additional unlabeled data. Many of these models use generative, probabilistic methods.
• Reinforcement learning – here no labeled data is available, but a method is used to quantify the machine’s performance in the form of rewards. The machine tries many different options and learns which actions are best based on the feedback (rewards) it receives.

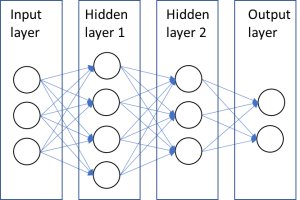
A common model used in machine learning is the artificial neural network. This is a model based on nodes connected by weighted edges, see for an example Figure 1. Commonly, the nodes are clustered in layers, and information is transported from the input layer to the output layer, traversing intermediate layers. These intermediate layers are the so-called hidden layers. The number of nodes per hidden layer can be chosen freely. For the input and output layer this will be determined by the preferred output and the number of inputs. At each node, the information is modified, based on a certain activation formula, for example a linear function or the sigmoid function, and the weights of the connecting edges. In the learning stage the weights or parameters are tuned such that the difference between the output data generated by the system and the desired output data is minimized.

The purpose of such a network can be classification and clustering of objects. It can also serve as a decision maker or as an associative or content-addressable memory, where a system recognizes specific patterns. This has applications in error correction where unwanted errors are automatically corrected, and anomaly detection, where suspicious behavior of parties in a network can be detected.

If we think how quantum computing and machine learning meet, we could think of both the input and the processing part being classical or quantum (Schuld & Petruccione, 2018 [1]). If both are classical, we have classical machine learning. Classical machine learning can be used to support quantum computing, for example in quantum error correction. Quantum processes can also be used as an inspiration for classical algorithms, such as  tensor networks, simulated annealing and in optimization.  If the input is a quantum-mechanical state and the computing is classical, the machine learning routine is used to translate quantum information into classical information. If both the input and computing are quantum, this will be real quantum machine learning, however, only a few results in this direction are published yet. In this article however, we look at classical input information and quantum processing.

One of the main benefits of quantum computers is the potential improvement in computational speed. Depending on the type of problem and algorithm, quantum algorithms can have a polynomial or exponential speed-up compared to classical algorithms. There are also other benefits relevant in the near future. Quantum computers could possibly learn from less data, deal with more complex structures or could be better in coping with noisy data. In short, the three main benefits of quantum machine learning are (interpretation based on Dunjko & Briegel, 2018 [2]):

• Improvements in run-time: obtaining faster results;
• Learning capacity improvements: increase of the capacity of associative or content-addressable memories;
• Learning efficiency improvements: less training information or simpler models needed to produce the same results or more complex relations can be learned from the same data.

For each of these benefits we show some examples further on in this article.

The improvement in run-time can be realized in various ways. Machine learning consists of optimization tasks that can be done faster by quantum annealers, like the D-Wave machine. Another way of getting a speed-up is the use of quantum sampling in generative models. Sampling is one of the tasks on which a quantum computer is expected to outperform classical computers already in the near future. Hybrid quantum-classical algorithms are expected to be among the first to outperform classical algorithms. Hybrid algorithms perform a part of the algorithm classically and a part on a quantum machine, using the specific benefits such as for example efficient sampling. The last way to realize the speed-up is via specific quantum machine learning algorithms using amplitude amplification and amplitude encoding. Amplitude amplification is a technique in quantum computing and is known to give a quadratic speed-up in comparison with classical approaches. In amplitude encoding, amplitudes of qubits are used to store data vectors exponentially efficiently, enabling exponential speed-up. However, this exponential speed-up is not obvious and the assumptions made to come to this theoretical speed-up have some technological challenges, (see e.g. Aaronson, 2015 [3]). Those quantum algorithms

• assume preloaded databases in quantum states, for example using quantum RAM (QRAM);
• assume data to be ‘relatively uniform’, meaning no big differences in value; and
• produce a quantum state as output, meaning this has to be transferred efficiently to a meaningful result.

As stated by Aaronson, 2015 [3]: ‘To maintain the potential exponential speedups of the quantum algorithms, this conversion needs to be efficient. If this is not the case, then one ends up in a situation in which the quantum algorithm can solve the problem very efficiently, but only after a lengthy preprocessing of the data has been performed, therefore killing the whole point of using the quantum algorithm.’ Otherwise one might be able to find a classical algorithm having similar performance. These issues, and the fact that the number of qubits is still small, makes that this class of specific quantum machine learning algorithms is still far away.

However, next to the mentioned improvements in run time, also capacity and efficiency improvements are benefits of quantum computing. In order to quantify the potential of both in improving machine learning, we implemented some examples from literature on the Quantum Inspire platform of QuTech, a joint venture of the Delft University of Technology and TNO, The Netherlands Organisation for applied scientific research. Each of those examples falls within a different combination of machine learning and expected benefit:

• Classification with Hybrid Helmholtz Machine (Benedetti, Realpe-Gómez, & Perdomo-Ortiz, 2018 [4]) – a generative semi-supervised learning model, expected to result in an improvement in run time using quantum sampling;
• Classification with Quantum Neural Networks (Fahri & Neven, 2018 [5]) – a supervised learning case, expected to result in an efficiency gain;
• Anomaly detection with Quantum Hopfield Networks (Rebentrost, Bromley, Weedbrook, & Lloyd, 2018 [6]) – a supervised learning case, expected to result in a capacity

In this article we will elaborate on the first example, a gate-based hybrid Helmholtz machine, whereas the original paper showed an implementation on the D-Wave annealer. This is the first time that a gate-based hybrid Helmholtz machine has been implemented.

The Quantum Inspire platform

Though building a quantum computer is one of the hardest quantum applications to reach, a lot of resources are put into its development throughout the world. Exploiting quantum mechanical effects such as quantum tunneling, superposition and entanglement, a quantum computer can be regarded as a massive parallel computation system capable of solving specific types of problems more efficiently than the classical computers. In general, two types of quantum computers are being developed: quantum annealing computers and gate-based quantum computers. The quantum annealing computers are sometimes referred to as analog quantum computers, where gate-based quantum computers are also called digital quantum computers.

Quantum annealing computers exploit the effect of quantum tunneling. Very simplified, this means that quantum mechanics allows very small particles such as electrons to go to the other side of a potential barrier by tunneling through that barrier, which is not possible classically. If you imagine a landscape full of hills and valleys and you are trying to find the lowest valley in this landscape, you can imagine that you can find this lowest valley faster if you could tunnel through the hills instead of climbing all the hills. The best known example of a quantum annealing machine is the D-Wave quantum computer. By controlling the potential landscape, annealing machines are capable of finding (approximate) solutions of various minimization problems.

Gate-based quantum computers can solve more general problems than annealing machines, but are more difficult to build and control. Gate-based quantum computers work by executing a quantum algorithm, which is a sequence of single-qubit and multi-qubit gates. A quantum gate is an operation on one or more qubits. Gate-based quantum computers exploit the quantum-mechanical properties of superposition and entanglement to create quantum algorithms potentially outperforming classical computers for various problems, such as big data analysis, machine learning, code breaking and even to assist in the quest for improved medicines or new materials with special properties. Qubits are the fundament of a gate-based quantum computer. Unlike classical bits, qubits can be in a superposition of 0 and 1. Qubits can also be entangled, meaning that the state of these qubits can no longer be described as separate qubits. The easiest way to think of this, is by an extension of the superposition principle: one qubit can be in the state 0 and 1 at the same time, two qubits can be in the states 00, 01, 10 and 11 at the same time, three qubits can be in the states 000, 001, 010, 011, 100, 101, 110 and 111 at the same time, etc. This means that an  qubit system can be in 2 to the power  possible states at the same time. When you do calculations with these entangles qubits, it is like you are operating on a massive parallel computer, performing operations on many bits at the same time. The finer details of quantum computing are much more complex than explained here. For the interested reader there is many literature online about the concept of quantum computing.

Quantum Inspire (QuTech, 2018 [7]) is an online quantum computing platform designed and built by QuTech ([7]) and is a gate-based quantum computing system. The goal of Quantum Inspire is to provide users access to various technologies to perform quantum computations and to provide insights in the principles of quantum computing. Quantum Inspire is a full stack system consisting of:

• a web portal with a GUI to program quantum algorithms in cQASM;
• a software development kit (SDK) that provides a Python interface to Quantum Inspire, a backend for the ProjectQ framework and a backend for the Qiskit framework;
• control software for scheduling and queueing jobs and for connecting the control hardware;
• software for data processing and automated tuning and calibration of quantum chips;
• different instances of the QX simulator for simulating up to 26 fully entangled qubits on a commodity server, or up to 37 fully entangled qubits on Cartesius, the Dutch national supercomputer.

Quantum Inspire is designed to be connected to both quantum simulators and quantum hardware.

At QuTech different qubit hardware technologies are being developed, such as superconducting charge qubits (transmons), semiconducting electron spin qubits and NV center qubits that are based on the spin properties of nitrogen-vacancy centers. Another line of development are qubits based on Majorana fermions. One or more of these quantum chips will be integrated in Quantum Inspire in the future, but they are not available for online access yet.

All work published in this paper has been executed on the QX simulator of Quantum Inspire. QX is a quantum computing simulator using vector state representation of qubit states and can be used to execute gate-based quantum algorithms. A primitive noise model for simulating depolarizing noise can be included in the simulation. The native gate set of cQASM contains single-qubit rotations of arbitrary angle around the 3 axes of rotation, standard two- and three-qubit operations (CNOT, CZ, Swap, Toffoli), but also binary controlled qubit operations.

What is a hybrid Helmholtz machine

Finding structure in data is hard. Humans are able to find structure, such as recognizing a handwritten digit, only because we have done it a thousand times. Even if the task seems naturally, everybody has had (and maybe even still has) a period in which he or she learned what all these writings mean. Computers can do similar things, but also have to learn first.

Often when information has to be obtained from data, specific machine learning tasks are used. Also for pattern recognition, machine learning algorithms are used to recognize and classify patterns. However, it is not true that every machine learning algorithm can be used to solve arbitrary tasks. In fact, specific tasks often require dedicated machine learning algorithms to find the answer.

A special class of machine learning algorithms are neural networks, where information is fed to a network or different nodes connected by weighted edges. A special neural network, which inspired the research on this topic, is the human brain. Also here, information that is obtained, for instance a sound we hear, activates some neurons. These neurons might activate other neurons, enabling us to recognize a sound as speech, music or noise.

Often, data fed to a neural network (either the human brain or artificial neural networks) are corrupted. Think for instance about an image of a pig with a crate partially in front of it. We do not see the full pig, however, we can still recognize it as being one. This task is harder for artificial neural networks. A special type of neural network suited for this specific task is a Helmholtz machine. Apart from trying to recognize patterns, a Helmholtz machine also tries to find probable explanations for certain patterns by means of pattern generation.

A Helmholtz machine consists of two neural networks. The first is a bottom-up recognition network, the second neural network is a top-down generative network. Data can only be given to the very first layer of the recognition network, and output is extracted from the last layer of the generative network. These layers, with which interaction is possible, are called visible. All layers with which no interaction is possible, are said to be hidden. Note that the first layer of the generative network is also hidden, as it gets input from the last layer of the recognition network (called sampling), meaning that users cannot interact with it. See also Figure 4 for an example of a Helmholtz machine with a visible layer of four nodes and a hidden layer with two nodes. Note that neural networks in general can have more than four nodes per layer, as well as more than one hidden layer. Data can be fed into the Helmholtz machine in the recognition network, and from the generative network data can be extracted.

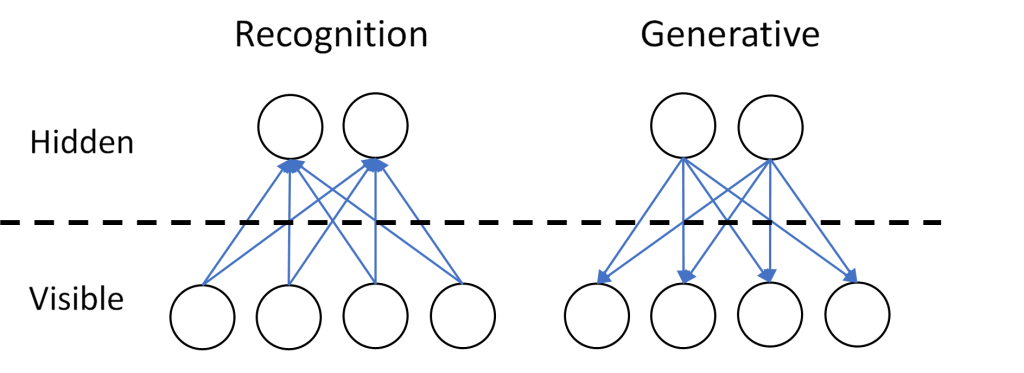
Each link has a weight assigned to it and based on the input and on the weight of links, other nodes can be activated. The hardest part that has to be executed in most neural networks, including the Helmholtz machine, is assigning the correct weight to each link.

This assignment of weights, which is also called learning, is performed iteratively. In general, data samples are presented to the neural network, after which the weights are updated to better fit all the data presented so far. For the Helmholtz machine, learning is slightly different as we have two neural networks working together instead of a single one. A special algorithm is used to train a Helmholtz machine and thus learn the weights of the links: the wake-sleep algorithm.

In the wake-sleep algorithm, the weights of both neural networks are learned alternately. A single iteration of learning consists of two phases. Firstly, the weights in the recognition network are fixed and the weights of the generative network are learned. The Helmholtz machine is in the wake-phase, as samples from the data set are used as input, this is also called sensing. Secondly, the weights in the generative  network are fixed, and the weights of the recognition network are learned. The Helmholtz machine is in the sleep-phase and gets is input by sampling from the probability distribution of the recognition network. This process is called dreaming.

Once the wake-sleep algorithm is finished, the Helmholtz machine is trained. It has learned an efficient representation of the data, often in the form of an approximate probability distribution, describing how often each pattern or event occurs.

Quantum computing can be used in multiple ways to enhance the Helmholtz machine. One way is by replacing the sampling in the first hidden layer of the generative network, by quantum sampling, as done by (Benedetti, Realpe-Gómez, & Perdomo-Ortiz, 2018 [4]). This approach gives a speed-up in running time, however uses a different computer paradigm, quantum annealing as explained in the previous section, than we use in this article. We consider a quantum-classical hybrid Helmholtz machine, where the neural networks are replaced by quantum gate-based neural network implementations, with classical pre- and postprocessing.

For this implementation, parameters used in the quantum circuit are learned instead of the weights of the links. Again, learning is done using the wake-sleep-algorithm. Theoretically, this approach requires less data samples and less training to achieve similar performance results.

Implementation of a hybrid Helmholtz machine on Quantum Inspire

A gate-based hybrid Helmholtz machine has been implemented on the Quantum Inspire platform, based on the work done in (Lopez-Chagoya, 2018 [8]). Every node in the classical network corresponds to a single qubit and the learned parameters, instead of weights, are used as input for operations on the qubits.

A gate-based quantum implementation of the recognition and generative network of Figure 4 is shown below in Figure 5 and Figure 6. Each line in these figures corresponds with a single qubit and each block corresponds with operations on that qubit. The parameters  are learned during the learning phase of the algorithm. This means that these parameters are similar to the weights in the classical Helmholtz machine.

The measurement results of the recognition circuit are used as input in the generative circuit. The operations connecting two qubits in the figures below correspond to the edges connecting two nodes in the classical neural network. With perfect training, and thus optimal parameters, the measurement results of the generative circuit match the probability distribution of the input data set.

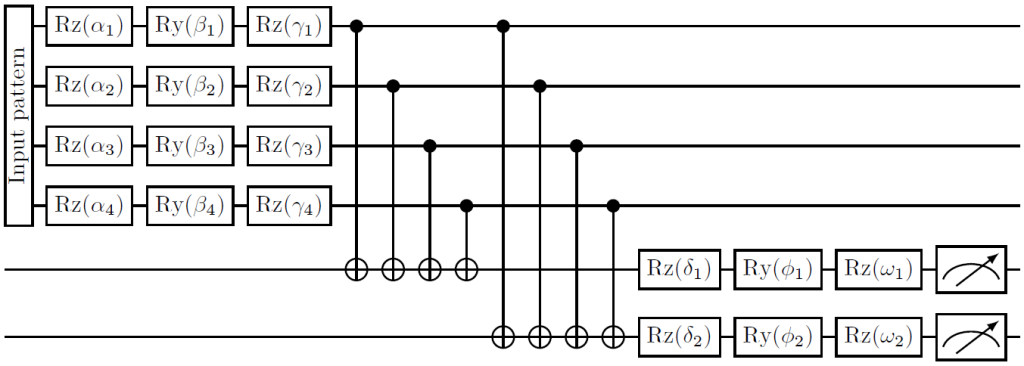
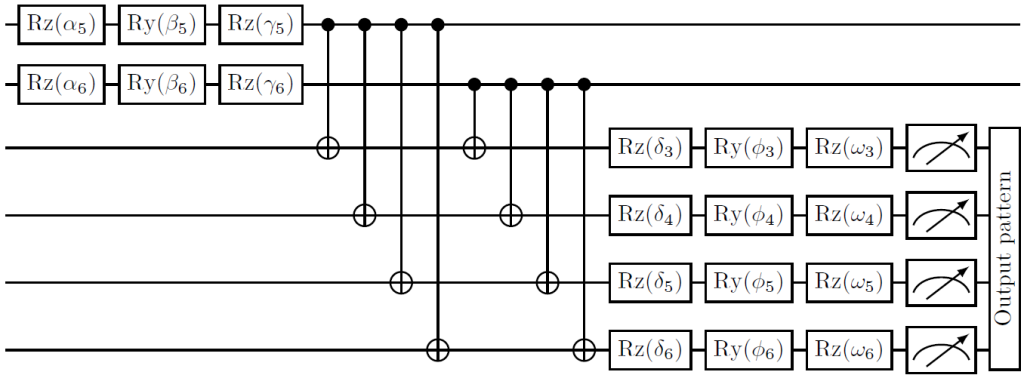
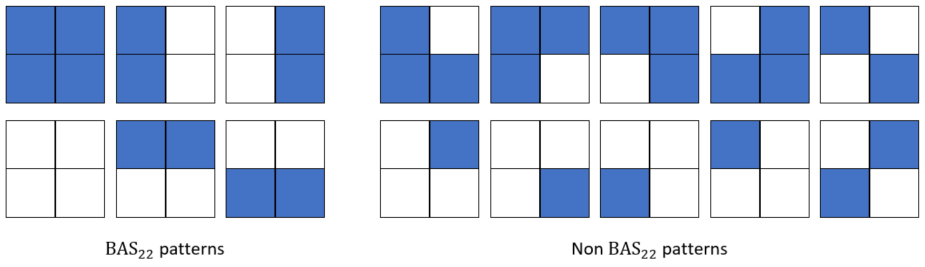
Both the recognition circuit and the generative circuit of the hybrid Helmholtz machine are implemented on the Quantum Inspire platform, based on the work done in (Lopez-Chagoya, 2018 [8]). As input for the recognition circuit, the -dataset is used (MacKay, 2003 [9]). The -dataset, short for Bars and Stripes-dataset, consists of 2-by-2 pixel images. In total there are sixteen possible 2-by-2 pixel images as shown in Figure 7, with the -dataset shown on the left only containing six of those.

The input of the hybrid Helmholtz machine are random samples from the -dataset. Each sample is transformed from a 2-by-2 pixel image to a binary string of length four, where a one represents a blue square and a zero a white square. The probability distribution for this dataset, describing how often each sample is chosen, is a discrete uniform distribution, meaning that each of the six images is equally likely to be chosen at random.

The hybrid Helmholtz machine tries to learn the probability distribution of the input set, meaning the hybrid Helmholtz machine tries to learn how often a 2-by-2 pixel image is likely to occur. This learning of the parameters by the hybrid Helmholtz machine happens in an iterative fashion. Each iteration consists of first learning the probability distribution of the input by trying to replicate the (fixed) output, and second, the other way around for the probability distribution of the output.

After learning the hybrid Helmholtz machine, it can be used to represent the input data efficiently. The performance of the machine is measured in terms of how good the output probability distribution matches that of the input. That is, how often each of the samples above occurs in the output. Note that the ten patterns that originally were not in the -dataset may still appear as output, given a suboptimal training of the parameters. Performance of both the classical and the hybrid Helmholtz machine is defined by the so-called Kullback-Liebler divergence, which indicates how well the probability distributions of the input and output match. The larger the Kullback-Liebler divergence is, the worse the two probability distributions match and the worse the performance is. When the output probability distribution is the same as the input, the Kullback-Liebler divergence equals zero and the Helmholtz machine has learned to reproduce the output with 100% accuracy.

Quantum hardware is still in development and running the hybrid Helmholtz machine requires too much resources. More qubits and more stable qubits are required, together with a link to a classical interface in order to train the hybrid Helmholtz machine. The hybrid Helmholtz machine can be simulated on a conventional computer, however at the cost of an increase in running time. Therefore, the number of learning cycles of the hybrid Helmholtz machine is limited.

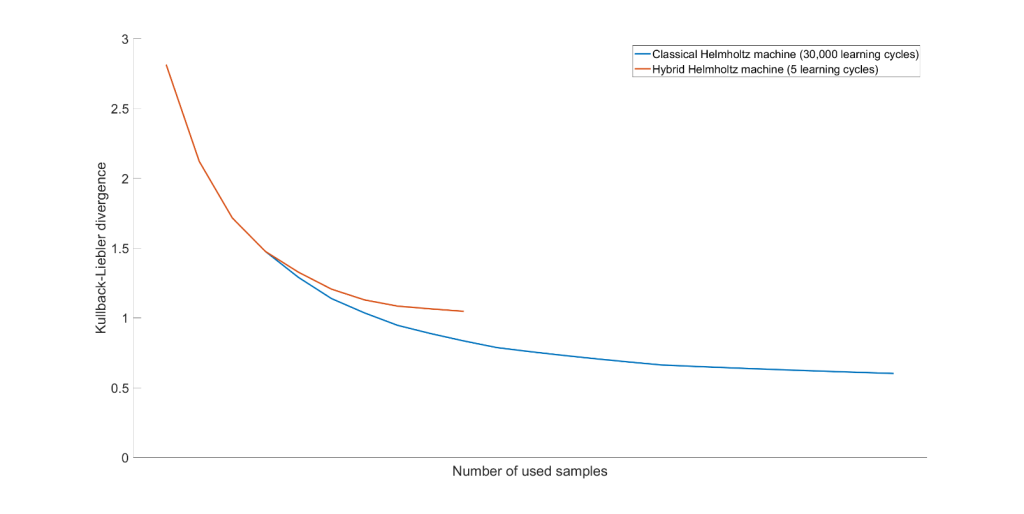
In Figure 8 we see results of both the classical Helmholtz machine and the hybrid Helmholtz machine in terms of the Kullback-Liebler divergence. On the horizontal axis the number of samples used is stated. Naturally, this number is larger for the classical Helmholtz machine than for the hybrid Helmholtz machine.

Based on these results we can conclude two things. The first being that it is indeed possible to implement a hybrid Helmholtz machine on a gate-based quantum computer. The second that more training cycles of the hybrid Helmholtz machine will probably also lead to better results, comparable to that of the classical Helmholtz machine.

Conclusion

In this article we discussed the possible effects of quantum computing on machine learning. Machine learning is applied in various areas: from pattern recognition to anomaly detection and from marketing to gaming. However, machine learning also has its limitations, such as the long running times and the restricted capacity. Using quantum computing, some of these challenges can be overcome.

Three ways can be identified in which machine learning can benefit from quantum computing. The first is run-time improvements. The second advantage is an increase in the capacity of associative or content-addressable memories. The third is more efficient learning. This means that quantum machine learning requires less data samples or less learning cycles to obtain similar or even better results.

In this article we focused on a specific machine learning algorithm: the Helmholtz machine. With both a recognition and a generative neural network, the Helmholtz machine is used to recognize patterns and to find explanations for corrupted input data. The Helmholtz machine learns iteratively an (unknown) probability distribution by trying to recognize patterns and generating new samples.

A Helmholtz machine benefits from quantum computing as it allows for more efficient learning. A hybrid classical-quantum Helmholtz machine was implemented on the Quantum Inspire platform, developed by QuTech in the Netherlands. This implementation is the first gate-based implementation of a hybrid Helmholtz machine. However, in this phase of the development of the quantum computer, a simulation of a quantum computer on a conventional (super) computer is used.

The Helmholtz machine was also implemented in a classical manner on a digital computer. Simulating the hybrid Helmholtz machine led to an increase in the running time, hence both implementations are not compared in terms of running time. Instead, the results are used to show that it is indeed possible to implement a hybrid Helmholtz machine in a gate-based manner. Performance was evaluated using the Kullbach-Liebler divergence, indicating how well the learned probability distribution matches that of the input.

We saw that the Kullbach-Liebler divergence decreased as the number of samples and the number of iterations increased for the classical Helmholtz machine. We also saw that the performance for the hybrid Helmholtz machine roughly followed that of the classical version for much less training iterations. We expect that with more iterations and improved quantum hardware the performance of the hybrid Helmholtz machine will improve and probably surpass that of the classical Helmholtz machine.

References

[1] Schuld, M., & Petruccione, F. (2018). Supervised Learning with Quantum Computers. Springer.

[2] Dunjko, V., & Briegel, H. J. (2018). Machine learning & artificial intelligence in the quantum domain: a review of recent progress. Reports on Progress in Physics 81.7.

[3] Aaronson, S. (2015). Read the fine print. Nature Physics 11.4, 291.

[4] Benedetti, M., Realpe-Gómez, J., & Perdomo-Ortiz, A. (2018). Quantum-assisted helmholtz machines: a quantum–classical deep learning framework for industrial datasets in near-term devices. Quantum Science and Technology 3.3.

[5] Fahri, E., & Neven, H. (2018). Classification with quantum neural networks on near term processors. arXiv preprint.

[6] Rebentrost, P., Bromley, T. R., Weedbrook, C., & Lloyd, S. (2018). Quantum Hopfield neural network. Physical Review A.

[7] QuTech. (2018). Quantum Inspire Home. Retrieved from Quantum Inspire: https://www.quantum-inspire.com/

[8] Lopez-Chagoya, T. J. (2018). Hybrid Helmholtz machine: A gate-based quantum circuit implementation. Maastricht, The Netherlands: Maastricht University: Master’s thesis.

[9] MacKay, D. J. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press.