The world of security and cryptography has been in relative peace until it became clear that Quantum Computing development will eventually result in usable devices. Both symmetric cryptography, for which two or more parties trust each other and possess the same key to accomplish security tasks, and that of asymmetric (or public key) cryptography have been relatively well understood. Security had been based on assumptions on the maximal power of an adversary that appeared more than reasonable. Many tools have been designed, found to be convenient and even certified from a practical security perspective and have relied on “provable” public key methods. These proofs have been based on an assumptions on complexity of specific tasks and from there the infeasibility of breaking the crypto methods in polynomial time has been deduced. Incidentally most of the wide spread public key methods have selected factoring big numbers into prime factors as the source of complexity. However, already in the ninety-nineties Peter Shor had put forward the “Shor-algorithm” that can solve in polynomial time the factorization problem on a sufficiently powerful Quantum Computer. Starting at the latest in 2013 the big security agencies, even NSA, have called for developing new methods that are “Quantum Safe”, i.e. secure against adversaries equipped with Quantum Computers.

Let us try to analyze the concept of Quantum Safety. There are two abstract possibilities (see Figure):

1. Quantum Safety in the narrow sense (i.e. secure to the best of our present knowledge on the computing efficiency of prospective Quantum computers). This is a Cryptography that is secure against known, cryptographically relevant, algorithms for Quantum Computers. At present these include the Shor algorithm and the Grover algorithm. The latter is a specific search algorithm. It essentially does not affect block-encryption schemes, such as AES, except for doubling of the key space, and these are therefore automatically Quantum Safe in the narrow sense.
2. Quantum Safety in a broad sense. It should not be breakable by a Quantum Computer at any future time. Naturally, this is not a well-defined category as:
   1. • the algorithms that can efficiently be executed on a Quantum Computer are principally unknown. It is often conjectured that the so called “NP hard problems” (at least as hard as any NP problem, the latter being a problem, unknown whether it can be solved in polynomial time, as function of its input, on a deterministic Turing machine) are also not solvable by a Quantum Computers in a polynomial time. In the end, however, this is only a conjecture and is based on what we do not know today; and
      • the method of application of a “Quantum Computer” is undefined. The “narrow sense” interpretation of a Quantum Computer implicitly assumes a kind of non-physical adversarial activity (although chosen plain attacks are not excluded), in which the communication, quantum and classical, data are supplied to a distant Quantum Computer that does calculations and provides the adversary with conclusions, e.g. the key generated in a Diffie-Hellman based protocol for subsequent direct decryption of any cipher text that is produced by a block–cipher encryption algorithm. Note, however, that this is not the only possibility, especially the attacks considered in physics-based crypto methods. More generally an adversary can possess a distributed quantum computer integrated in the user’s infrastructure that also steers physical attacks.

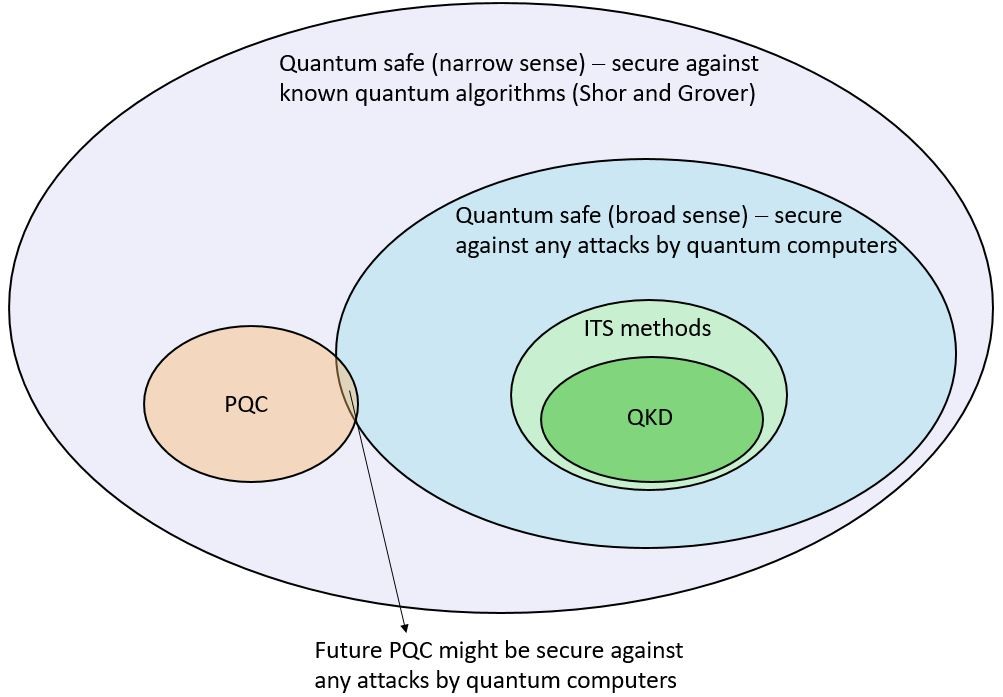
The presently known Quantum safe methods include:

1. Post-Quantum Cryptography (PQC).

Post Quantum Cryptography as presently evaluated at NIST is a set of public key algorithms. All these algorithms are related to different classes of problems, which are different from the factoring problem as well as the related discrete logarithms and elliptic curves which .are “easily solvable” by the Shor algorithm for universal Quantum Computers in the above sense. The post-quantum public key algorithms therefore are Shor-secure. It is not known publicly, whether these other fundamental problems suggested as foundational for different post-quantum versions may be susceptible to yet unknown algorithms for Quantum Computers.

However, there is a sentiment that the problems lying at the heart of present day post-quantum cryptography might have been too exotic to be addressed by a sufficient amount of researchers developing Quantum Computing algorithms up to now. This is of course a speculation. The fact is that post-quantum public key cryptography is designed to be Shor-safe and is thus Quantum Safe in the narrow sense.

2. Quantum Key Distribution (QKD).

QKD is a key generation method that uses quantum mechanical effects to establish security. There are different possibilities to address

• In the most traditional sense QKD (put forward already in 1983 with some intuitions existing before) is considered as an Information Theoretically Secure (ITS) primitive (i.e. secure forever against any completely unlimited eavesdropper except for a negligible probability ε that can be reduced at will) with potential implementation imperfections. This is a very appealing interpretation as in theory implementation imperfections are nothing special – any crypto primitive has some qualities that are “spoiled” by implementation imperfections. Clearly an ITS scheme cannot be thwarted by any algorithm whatsoever, and not by any attack, irrespective of its specific realization (distributed or not). So clearly, in this interpretation, QKD is Quantum Safe in a broad sense.

Note: This property is restricted to key generation alone.

• QKD as a Quantum Safe Implementation in a narrow sense. It can be argued (see box) that from a security point of view, QKD is not worse than any narrow-sense Quantum Safe method. QKD is also forward secure (as most physical methods), sometimes called everlasting secure, i.e. that if it is not broken in real time, it cannot be broken later in any way. This feature is a significant improvement to all present day and Post-Quantum methods, as the output of these can be passively eavesdropped, stored and, potentially, broken later. However, we should seriously address also the practical side of QKD. On security-management levels there is the prejudice that QKD is difficult to operate, needs parallel communication infrastructures (optical fiber networks) and mainly therefore (OPEX) but also as of itself (CAPEX) is inherently and forbiddingly expensive. Some people believe: “If QKD is not ITS, it cannot be sold to the management.” This is sort of skepticism is confirmed by existing products on the market. However, it is clear that this is a result of extreme narrow proliferation in niche markets and lack of sufficient R&D investment with practical orientation. Moreover, there exist examples of QKD technology that are much more convenient to use, do not require a parallel infrastructure and are significantly cheaper already now. It is also arguable, although not everyone agrees, that leaving aside some traditional ITS requirements that non-ITS QKD variants can get even more efficient and less expensive. On the positive “popular side” there are arguments by security practitioners: “We do not want something ideal (ITS). We do want something that is dauntingly difficult (practically unrealistic) to crack and we want to use such a method jointly with Post-Quantum methods. In this way we would have a ‘software’ backed and a ‘hardware’ backed security, sort of ‘unbeatable’ two factor crypto as of today.”

Real Security and real security of QKD

Security of traditional crypto devices

Core Crypto Primitives: There are two types of crypto primitives – those based on provable security (as is e.g. public key crypto or QKD) and others based on the lack of knowledge of feasible attacks (as are block cyphers, e.g. AES). We shall review in more detail the first class here: as in any theorem there are assumptions and then a proof that is a mathematical derivation, the result of course being an implicit but direct consequence of the assumptions. In the case of public key cryptography, as already mentioned, the assumption is the complexity of a problem i.e. that for known algorithms, the inverse of an “easy” problem is of higher than polynomial complexity (as function of the length of the input). Meanwhile experts in the field have shown that there is a lot of progress in this domain (different for the specific different crypto primitives) and while the conjecture still holds it is greatly eroded even in the domain of traditional mathematical algorithms.

Implementation: It can be argued that in the case of mathematical cryptographic algorithms the core primitive is not affected by implementation as the assumptions are not. No doubt, implementation opens side channels but these can be independently tackled, by methods that do not affect the core primitive. Unfortunately this does not hold for QKD as it is a physics-based primitive. Indeed implementation affects the assumptions (particularly the first one) and then there is no easy way to prove security with unstable assumptions on system models, especially in the case of system models of increasing complexity.

QKD security

Core Primitive of QKD: The security of QKD is rooted in assumptions, most notably knowledge of the model of the QKD system, authentic message communication, availability of true random number generators, and absolute security isolation. Derivations of security proofs follow the rules of Quantum Information Theory (i.e. the hidden assumption is that Quantum theory is “correct” something that we are not going to doubt here).

The Security of QKD implementations:

There are two problems of QKD implementations.

First, there are problems related to the model that in contrast to traditional security devices IS NOT unrelated to the implementation – i.e. the core primitive and the implementation are intertwined. Irrespectively of how much effort is put here (closing the obvious side channels or attempting a Security Proof to the best of our knowledge on an extended model and at the expense of decreased performance) QKD will not become secure “by the laws of nature” but rather will be a function of our description of the system. However, no matter what a QKD system cannot be broken by a distant (physically passive) computing machine running any algorithms. The machine cannot use side channels at all even if they are not closed! (This already goes at least partially in the broad sense Quantum Safety.) To break QKD one needs an elaborate and advanced, quantum attacks with direct access to the quantum channel.

Second, the isolation assumption is not reasonable as in a strict sense it would render the QKD system unusable. This problem can be avoided by using additionally post-quantum only methods and/or adequate additional isolation by organizational measures. In any case QKD will remain Quantum Safe at least in the narrow sense.

What higher security can QKD aim at beyond Quantum Safety in the narrow sense?

This is a really difficult point.

In this connection it should be considered whether cheaper and more efficient devices that are only quantum safe in the narrow sense are not worth addressing.

Moreover, it can aim at “everlasting security” if methods used that are not everlasting secure are ensured not to have an impact on key generation (possibly with organizational methods).

If we close all known side channels we shall render QKD Quantum Safe in the broader sense to the best of our knowledge. We can go even for something as ITS “to the best of our knowledge” attempting a model that captures all known side channels at any given point of time. Might be such security is not worth the effort from a practical point of view. However, this is a very interesting research line that might bring us to new insights.

At the same time the struggle for low cost, increased efficiency and applicability must continue. Last but not least we would mention that security design of QKD networks is critical as this is an essential part of realistic, non-niche applicability.

3. Quantum Cryptography beyond QKD

QKD is just a key generation method – nothing more. It is an essential building block in symmetric cryptography. We know, however, that it is asymmetric cryptography (in terms of use cases not methodology) that is needed to solve many of the real security problems in the modern world. Asymmetric tasks can be efficiently solved by means of public key cryptography, for which reason PQC is indispensable.

However, asymmetric Quantum Cryptography is a field of research that exists, is viable, although it is little known as of today.

All started with an early observation / proof of H.-K. Lo in the 90s that ITS asymmetric cryptography is impossible by quantum means. This led to complete disinterest to the subject among Quantum Information scientists. However, around 2005 L. Salvail came with an ingenious scheme. If one uses QKD hardware, changes the post-processing and assumes an eavesdropper with limited quantum resources (limited quantum storage or noisy quantum memory) then he/she can realize bit-commitment and oblivious transfer – the sufficient building blocks for realizing any asymmetric crypto primitives. Later preliminary experimental tests of these protocols and extensions to identification (C. Schaffner et al.) have been carried out. Unfortunately, hitherto these themes have remained very little studied.

The bottom-line is that there is a significant but not sufficiently studied potential for QKD hardware to be used for classes of cryptography other than key generation. It appears that the resulting schemes, even if not ITS would probably turn out to be Quantum Safe.