“Nature isn’t classical, dammit, and if you want to make a simulation of nature, you’d better make it quantum mechanical, and by golly it’s a wonderful problem, because it doesn’t look so easy”                                       
                                                                                               — Richard Feynman

In diesem Artikel erklären wir, warum Quantencomputer hilfreich sind, um komplexe Moleküle zu beschreiben. Aus Gründen der Lesbarkeit und um den Artikel für eine breite
Leserschaft zu öffnen, verzichten wir auf genaue mathematische Beschreibungen und auf die Erklärung wichtiger Techniken wie beispielsweise der Jordan-Wigner-Transformation oder der Beschreibung fermionischer Hamiltonians. Hingegen setzen wir ein Grundverständnis der Eigenschaften von Qubits voraus. Für eine mathematische und vollständige Einführung empfehlen wir die Review-Artikel [1, 2].

1. Quantenchemie und Pharmaforschung

Medikamente sind chemische Stoffe, die im menschlichen oder tierischen Körper eine gewünschte Wirkung, zum Beispiel die Hemmung eines Proteins, auslösen. Dazu muss das Medikament in der Lage sein, an körpereigene Moleküle wie Proteine oder DNA mittels Atom- und Molekül-Wechselwirkungen spezifisch zu binden.

Um herauszufinden, ob potenzielle Medikamente dazu in der Lage sind, werden nach der aufwendigen Synthese des Moleküls zur genaueren Untersuchung viele Experimente (in vitro – im Reagenzglas) durchgeführt. Diese Experimente sowie die Synthesen sind sowohl zeitaufwendig als auch kostenintensiv. Wäre man in der Lage, solche Experimente durch andere Methoden zu ergänzen oder sogar vollständig zu ersetzen, wäre es möglich,
Medikamente deutlich schneller und effizienter zu entwickeln.

Durch die immer leistungsstärker werdenden Computer war es in den letzten Jahrzehnten möglich, Experimente mit Simulationen auf Computern zu ergänzen. Um vorherzusagen,
ob z.B. ein Molekül an ein Protein bindet, muss man allerdings in der Lage sein, beide Systeme sehr genau zu beschreiben, was viel Rechenleistung benötigt.

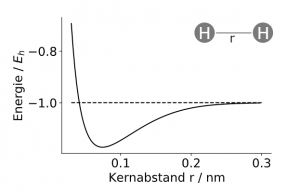
Um beispielsweise einen Computer dazu zu benutzen, die Frage, ob zwei Atome eine Bindung eingehen, zu beantworten, kann man den Computer eine Potentialkurve berechnen lassen. Die Potentialkurve kann man sich analog dem Verlauf der potentiellen Energie eines Balls in einem Gebirge vorstellen. Auf einem hohen Berg hat der Ball eine höhere potentielle Energie als im tiefsten Tal. Bei zwei Atomen entsteht diese Kurve durch
die verschiedenen Abstoßungs- und Anziehungskräfte der verschiedenen Teilchen. In Abbildung 1 zeigen wir den Verlauf der Potentialkurve für zwei Wasserstoffatome. Für kurze Entfernungen von beiden Atomen wird das Geschehen von der Abstoßung der beiden positiv geladenen Kerne und quantenmechanischen Kräften dominiert. Für große Kernabstände überwiegen die anziehenden Kräfte zwischen den negativ geladenen Elektronen und positiv geladenen Kernen. Die Potentialkurve in Abbildung 1 zeigt für verschiedene Abstände der beiden Atome die Energie des Gesamtsystems. Wir finden bei einem Abstand von (r = 0.0741 nm = 0.741 Å )das Minimum der Potentialkurve, an diesem Punkt gleichen sich abstoßende und anziehende Kräfte aus! Wir haben also herausgefunden, dass zwei Wasserstoffatome sich gerne nah beieinander aufhalten, also eine Bindung eingehen und ein Wasserstoffmolekül bilden. Für solch ein relativ einfaches Molekül stellt die Berechnung der Potentialkurve auf einem klassischen Computer noch kein zu großes Problem dar. Je größer die Systeme sind, desto unzuverlässiger werden die Simulationen auf Computern. So kann es auch zu völlig falschen Vorhersagen kommen, ob Moleküle tatsächlich aneinander binden.

2. Warum Quantencomputer?

In den letzten Jahrzehnten wurde bei der quantenchemischen Simulation auf klassischen Computern viel Fortschritt gemacht. Trotz der vielen Näherungsmethoden, die eingeführt wurden, bleibt die Komplexität der Quantenmechanik schwer zu bewältigen. Zudem führen die vielen eingeführten Näherungen dazu, dass berechnete Vorhersagen nicht immer zuverlässig sind. Das Aufkommen der Quantencomputer und die Verwendung ihrer einzigartigen Eigenschaften wird die Simulation von Quantenchemie in den kommenden Jahrzehnten revolutionieren. Quantencomputer werden bei vielen wichtigen Problemen in der Quantenchemie, wie zum Beispiel der Berechnung der elektronischen Struktur von Molekülen, effizient genaue Ergebnisse liefern. In den letzten zwei Jahrzehnten wurden bei der Entwicklung von Algorithmen und physikalischer Hardware für Quantencomputer bedeutende Fortschritte erzielt.

Wir erwarten dass die Simulation von Molekülen die erste wirkliche Anwendung sein wird, bei der Quantencomputer ihre beispiellose Rechenleistung zeigen können.

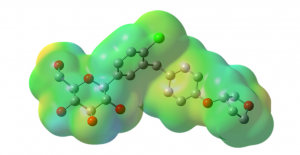
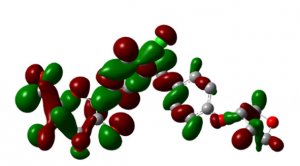
In Abbildung 2 zeigen wir eine Darstellung des Empagliflo-zin-Molekül inklusive seiner Elektronenverteilung, ein Wirkstoff zur Behandlung des Diabetes Typ 2. Dieses Molekül besteht aus 58 Atomen und insgesamt 235 Elektronen. Die Elektronen wechselwirken elektrostatisch und quantenmechanisch miteinander, was Auswirkungen auf die Struktur und Eigenschaften des Moleküls hat. Wenn sich ein Elektron bewegt, spüren alle anderen Elektronen diese Bewegung und reagieren darauf.

Die benötigten Ressourcen auf einem Computer, die für die Simulation eines Moleküls benötigt werden, steigen exponentiell mit der Anzahl der quantenmechnanischen Teilchen, der Elektronen, an. Aufgrund dieser exponentiell wachsenden Komplexität sind Moleküle auf klassischen Computern nur mit Näherungen zu beschreiben. Um ein Molekül wie in Abbildung 2 exakt zu berechnen, würde es Computerresourcen benötigen, welche weder heute verfügbar sind noch in absehbarer Zukunft verfügbar sein werden.

Der Nobelpreisträger Richard Feymnan hat deshalb schon 1982 vorgeschlagen anstatt klassischer Computer quantenme-chanische Systeme zu benutzen um andere quantenmecha-nischen Systeme, wie beispielsweise Moleküle, effizient zu simulieren [4]. Ein solches quantemmechanisches System ist der Quantencomputer.

3. Wie kommt das Molekül auf den Quantencomputer?

Auch wenn sich Quantencomputer und klassische Computer grundlegend unterscheiden, sind beides technische Systeme die dafür genutzt werden sollen Lösungen von komplexen Problemen zu finden. Die Aufgabe als Benutzer dieser Systeme ist es das gewünschte Problem mathematisch so zu formulieren dass es auf einem Computer effizient berechnet werden kann. Hier erklären wir wie das Problem der Beschreibung eines Moleküls, dem Wasserstoffmolekül, aussieht, zeigen wie es auf einem Computer beschrieben werden kann und warum die Darstellung auf einem Quantencomputer effizienter ist als die Darstellung auf einem klassischen Computer.

3.1 Moleküle und Quantenphysik

In der Realität bestehen Moleküle aus Elektronen und Kernen, welche aus Neutronen und Protonen bestehen. Als zu Beginn des 20. Jahrhunderts versucht wurde die Bewegung der Elektronen und der Kerne zu beschreiben wurde festgestellt dass die klassische Physik nicht in der Lage ist theoretische Vorhersagen zu liefern die den experimentellen Ergebnissen entsprechen. Man entwickelte eine neue Theorie zur Beschreibung solcher System: die Quantenphysik. In der klassischen Physik beschreibt man Objekte mit einem Ort und einer Geschwindigkeit – während in der Quantenphysik Teilchen an keinen bestimmten Ort sondern über den Raum verteilt sind, was durch die sogenannte Wellenfunktionen Ψ(r) beschrieben wird. Das Quadrat einer solchen Wellenfunktion (|Ψ(r)|^2) beschreibt die Wahrscheinlichkeit das Teilchen an einem bestimmten Ort r im Raum zu finden. In Experimenten wurde außerdem festgestellt dass, anders als in der klassischen Welt, quantenmechanische Systeme nicht beliebige kontinuierliche Energien besitzen können. Die Energien sind gequantelt – es existieren nur bestimmte, diskrete Energiestufen.

Um solche diskreten Messergebnisse zu beschreiben verwenden wir in der Quantenphysik Operatoren. Operatoren sind nicht nur einfache Zahlen sondern beschreiben mathematische Operationen auf Funktionen, wie beispielsweise eine Ableitung. Wendet man Operatoren auf eine Wellenfunktion an, wird diese sich verändern. Zum Beispiel kann ein Operator die Wellen-funktion im Raum verschieben oder ihre Form ändern. Dadurch ändert sich auch die Wahrscheinlichkeit ( |Ψ(r)|^2 ) das Teilchen an einem bestimmten Ort r zu finden. Der wichtigste aller Operatoren ist der Energieoperator, oder Hamiltonian, welcher die Information über die Energiebeiträge im System, wie zum Beispiel die Bewegungsenergie und die potentiellen Energien enthält. Der Hamiltonian beschreibt, welche diskreten Energi-enwerte wir im Experiment messen können. Um die möglichen Messergebnisse zu finden, müssen wir ein mathematischen Problem lösen: wir müssen die Wellenfunktionen finden, welche unter der Anwendung des Hamiltonians ihre äußere Form nicht ändern. Diese spezielle Klasse von Wellenfunktionen nennen wir Eigenfunktionen des Hamiltonians und jeder Eigenfunktion können wir eine diskrete Energie zuweisen.

Das mathematische Problem das wir gerade beschrieben haben wird in der Schrödinger-Gleichung $$ HˆΨ(r) = EΨ(r) $$ abgebildet. Auf der linken Seite, (HˆΨ(r)), wirkt der Hamiltonian auf eine Wellenfunktion, auf der rechten Seite, (EΨ(r)), steht dieselbe Wellenfunktion multipliziert mit der dazugehörigen Energie E. Die Schrödinger-Gleichung gilt also wenn die Aktion des Hamiltonians die Wellenfunktion bis auf einen Faktor, nämlich der Energie E, unverändert lässt. Anstatt Eigenfunktionen werden diese Wellenfunktionen dementsprechend auch Lösungen der Schrödinger-Gleichung genannt.

3.2 Das Wasserstoffatom

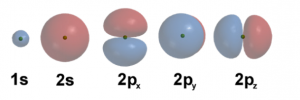
Für jedes System, sei es großes Molekül, ein kleines Atom oder gar ein einzelnes Elektron, konnen wir eine Schrödinger-Gleichung aufstellen. Für jede Schrödinger-Gleichung beschreibt der Hamiltonian Hˆ die verschiedenen Energiebeiträge des Systems. Als Beispiel schauen wir uns das Wasserstoffatom, H, an, welches aus einem Proton und einem Elektron besteht. In diesem Fall enthält der Hamiltonian Hˆ die Information über die Bewegungsenergie der Teilchen sowie die Wechselwirkung des Elektrons mit dem Kern. Wir müssen nun herausfinden, welche Wellenfunktionen die Schrödinger-Gleichung für dieses System lösen. Für ein einzelnes Wasserstoffatom konnen wir die Lösungen nach einer mathematischen Rechnung ohne Hilfe eines Computers finden [6]. Aus allen Lösungen können wir dann die Wellenfunktion mit niedrigster Energie bestimmen – und finden so den energetischen Grundzustand des Atoms. Für das Wasserstoffatom nennen wir diese Lösungen auch Atomor-bitale. Da jede Wellenfunktion einen Zustand des Elektrons im drei-dimensionalen Raum beschreibt können wir die Lösungen auch bildlich darstellen, siehe Abbildung 3 für eine Auswahl der Wahrscheinlichkeitsverteilungen (|Ψ(r)|^2).

Damit haben wir das Elektron allerdings noch nicht voll-ständig beschrieben. Elektronen, anders als makroskopische Objekte, besitzen neben ihrer Beschreibung im drei-dimensi-onalen Raum noch einen weiteren Freiheitsgrad: den Spin. Der Spin ist ein rein quantenmechanisches Konzept und hat keinerlei klassische Interpretation – jedoch kann man ihn als intrinsische Eigenrotation des Teilchens sehen. Diese Eigenrotation kann nur zwei Werte annehmen, entweder der Spin zeigt nach oben (spin up: ↑) oder nach unten (spin down: ↓). Zusammen mit der räumlichen Komponente beschreibt die Spin-Komponente das Atom vollständig.

3.3 Die Elektron-Elektron-Wechselwirkung und das Pauli-Prinzip

Im Vergleich zu allen anderen Atomen des Periodensystems besitzt das Wasserstoff ein Alleinstellungsmerkmal: es ist das einzige Atom mit nur einem Elektron. Andere Atome besitzen viele Elektronen, beispielsweise besitzt Lithium, Li, 3 Elektronen oder Cäsium, Cs, 55 Elektronen. In solchen System gibt es natürlicherweise Wechselwirkungen zwischen Elektronen, welche im Hamiltonian und damit in der Schrödinger-Gleichung beschrieben werden müssen. Des weiteren gilt für Systeme mit mehreren Elektronen ein weiteres quantenmechanisches Gesetz: das Pauli-Prinzip. Dieses Gesetz besagt, dass zwei Elektronen niemals von der exakt gleichen Wellenfunktion und selber Spin-Ausrichtung beschrieben werden können. Die Wellenfunktion von zwei Elektronen muss sich sich also entweder in ihrer räumlichen oder ihrer Spin-Komponente unterscheiden. Zum Beispiel dürfen zwei Elektronen mit derselben Spin-Ausrichtung nicht von der selben räumlichen Wellenfunktion beschrieben werden. Die komplizierten Elektron-Elektron-Wechselwirkungen sowie das Pauli-Prinzip machen die Lösung der Schrödinger-Gleichung für Systeme mit mehr als einem Elektron viel aufwändiger als für ein ein-zelnes Wasserstoffatom mit nur einem Elektron. Bereits das Wasserstoffmolekül, (H_2), kann nicht mehr exakt beschrieben werden, sondern muss vereinfacht werden und benötigt die Hilfe von Computerprogrammen.

3.3.1 Näherungen

Eine erste wichtige Näherung ist die Born-Oppenheimer-Nähe-rung. Da ein Proton etwa 2000 mal schwerer ist als ein Elektron, beeinflussen die Elektronen die Bewegung der Kerne kaum. Wir können die Kerne also als ruhend annehmen und unser Problem vereinfacht sich auf das Problem der Beschreibung von Elektronen im Einfluss der ruhenden Kerne. Die komplizierte Elektron-Elektron-Wechselwirkung bleibt allerdings weiter Teil des Problems. Eine offensichtliche, aber drastische Vereinfachung ist es diese Wechselwirkung vollständig zu ignorieren. Die Wellenfunktionen welche wir unter dieser drastischen Vereinfachung finden, sind keine exakten Lösungen der Schrödinger-Gleichung und auch die berechneten Energien weichen stark von experimentellen Werten ab.

Anstatt die Elektron-Elektron-Wechselwirkung vollständig zu ignorieren ist es besser sie näherungsweise zu beschreiben. Hierfür gibt es verschiedene Ideen und Ansätze. Die wohl be-kannteste Methode ist die Hartree-Fock-Methode, siehe [7]. Das Resultat der Hartree-Fock-Methode sind, analog zu den gefunden Atomorbitalen des Wasserstoffatoms, Molekülorbitale, welche benutzt werden können um eine näherungsweise Lösung der Schrödinger-Gleichung zu finden. Für komplexere Systeme wie beispielsweise dem Empagliflozin-Molekül können die Mole-külorbitale sehr komplexe Strukturen und Formen annehmen, siehe Abbildung 4 für die grafische Darstellung eines einzelnen Molekülorbitals von Empagliflozin. Die Hartree-Fock-Methode liefert für schwach wechselwirkende Moleküle eine gute An-näherung an den Grundzustand der Schrödinger-Gleichung.

Ein weiterer Vorteil ist dass die benötigte Rechenleistung für die Hartree-Fock-Methode auf klassischen Computern moderat ist, was es ermöglicht Berechnungen auch für große Moleküle mit vielen Elektronen auszuführen. Für manche Moleküle ist die exakte Wechselwirkung der Elektronen allerdings von entscheidender Bedeutung für die Beschreibung des Moleküls. In solchen Fällen liefert die Hartree-Fock-Methode keine zu-friedenstellende Ergebnisse mehr.

 

3.3.2 Auf dem Weg zur exakten Lösung

 

Die Hartree-Fock-Methode

Die Hartree-Fock-Methode erlaubt den energetischen Grundzustand der Schrödinger-Gleichung näherungsweise zu bestimmen. Hierfür werden die Elektron-Elektron-Wechselwirkungen nicht explizit beschrieben. Elektronen wechselwirken nicht mehr direkt miteinander, sondern spüren die Wechselwirkung durch ein elektrostatisches Feld welches von allen anderen Elektronen erzeugt wurde (mean-field approach). Jedes Elektron kann also wieder durch eine eigene Schrödinger-Gleichung beschrieben werden. Löst man diese Schrödinger-Gleichung erhält man einen neuen Zustand – und eine neues Feld. Man wiederholt dieses Verfahren iterativ bis sich die Felder nicht mehr a¨ndern. Am Ende der Berechnung erhalten wir Molekülorbitale. Besetzen wir die Molekülorbitale mit niedrigster Energie unter Beachtung des Pauli-Prinzips, erhalten wir eine Wellenfunktion welche (näherungsweise) den Grundzustand der Schrödinger-Gleichung darstellt. Die mögliche Besetzung der Molekülorbitale kann mit Hilfe der Dirac-Schreibweise anschaulich dargestellt werden. Das Pauli-Prinzip erlaubt dass ein Molekülorbital mit einem Elektron mit spin down (↓) und einem Elektron mit spin up (↑) besetzt werden kann: in jedem Molekülorbital ist also Platz für zwei Elektronen. Für zwei Molekülorbitale haben wir also vier freie Plätze um ein Elektron zu platzieren. Der Grundzustand in der Dirac-Schreibeweise kann also als |↓↑, □□> dargestellt werden – wir haben das erste Molekülorbital mit einem Elektron mit spin down und einem Elektron mit spin up besetzt. Die beiden Plätze im zweiten Molekülorbital bleiben unbesetzt (□).

 

Es existieren viele Methoden welche ausgehend von den Molekülorbitalen versuchen bessere Lösungen zu finden. Solche Post-Hartree-Fock -Methoden liefern häufig bessere Resultate sind aber auch deutlich rechenintensiver und deshalb meist nur für kleine Systeme möglich. Ein Beispiel für solche Methoden ist die Full Configuration Interaction (FCI)-Methode, siehe [7].

Die FCI-Methode benötigt auf einem Computer viele Ressourcen. Für ein Molekül mit n Elektronen und N Molekülorbitalen benötigen wir exponentiell viele Koeffizienten, um die FCI-Methode zu implementieren. Diese Koeffizienten müssen wir auf einem klassischen Computer speichern. Nehmen wir an, dass jeder Koeffizient mit einer Präzision von 128 Bits gespeichert wird, benötigten wir für n = 20 Elektronen und N= 40 Molekülorbitale 4 Terabyte an Arbeitsspeicher. Für n =50 Elektronen und N = 100 Molekülorbitale sind es bereits 1018Terabyte, ein Wert, welcher viele Größenordnungen über dem verfügbaren Arbeitsspeicher des größten Superrechners liegt.Im Gegensatz ist dieselbe Darstellung auf einem Quantencomputer dank Superposition deutlich effizienter. Für Moleküle mit n Elektronen in N Molekülorbitalen benötigen wir nur N Qubits – eine deutliche Ersparnis gegenüber der Darstellung auf einem klassischen Computer!

Die Darstellung eines Moleküls auf dem Quantencomputer ist allerdings nur der erste Schritt. Als nächstes muss man auf dem Quantencomputer den Grundzustand suchen. Dazu benutzt man Quantenalgorithmen, beispielsweise den Variational Quantum Eigensolver (VQE) [8], einen Quantenalgorithmus für Quantencomputer mit wenigen Qubits und ohne Fehlerkorrektur, oder Quantum Phase Estimation (QPE) [9, 10], einen Quantenalgorithmus für fehlerkorrigierte Quantencomputer. Mit solchen Algorithmen ist man dann in der Lage, den Grundzustand eines komplexen Moleküls für verschiedene Kernabstände zu finden, kann damit exakte Potentialkurven berechnen und genau vorhersagen, ob zwei Moleküle binden. Bis dies Realität wird, wird es allerdings noch einige Jahre dauern. Die bisherigen Quantenchemie-Berechnungen auf Quantencomputern wurden aufgrund der geringen Anzahl von verfügbaren Qubits und den hohen Fehlerraten nur für kleine Moleküle wie beispielsweise (BeH_2) [11] oder Wasserstoffketten [12] durchgeführt. All diese ersten Berechnungen könnte man auch problemlos auf heutigen klassischen Computern ausführen. In den nächsten Jahren wird die Anzahl der Qubits weiter steigen, die Fehlerrate sinken und es wird möglich sein, Berechnungen auszuführen, welche auf klassischen Computern undenkbar wären.

In Zukunft könnte man Quantencomputer dann beispielsweise dazu nutzen, um das in Abbildung 2 gezeigte Empagliflozin-Molekül akkurat zu beschreiben. Dies wäre der erste Schritt in Richtung einer neuen – von Quantencomputern unterstützten – Art der Medikamentenentwicklung. Für echte bahnbrechende Innovationen müssten im Anschluss allerdings viele weitere Forschungsfragen beantworten werden, zum Beispiel wie man das Molekül mithilfe eines Quantencomputers nicht nur im Vakuum, sondern auch im Umfeld des menschlichen Körpers beschreiben könnte. Hierzu müssten dann nicht nur leistungsstärkere Quantencomputer gebaut, sondern auch bessere Quantenalgorithmen entwickelt werden.

Zusammenfassend war das Ziel dieses Artikels, einen ersten Einblick in die Welt der Moleküle zu geben und zu erklären, wie diese auf einem Quantencomputer dargestellt werden können. Die hier gewählte Darstellung mittels Molekülorbitalen ist allerdings
nur eine vieler Möglichkeiten, ein Molekül darzustellen.

Ebenso gibt es viele weitere Methoden für klassische Computer, welche gute Näherungen erzeugen können. Wichtige Beispiele solcher Methoden sind die Dichtefunktionaltheorie (DFT), Coupled Cluster-Methoden (CC) oder das Møller-Plesset-Verfahren, siehe [7]. In den nächsten Jahren, wo die Rechenleistung der Quantencomputer aufgrund der geringen Anzahl von Qubits beschränkt sein wird, ist es dementsprechend wichtig, Probleme zu identifizieren, welche mit diesen klassischen Methoden nicht mehr akkurat genug dargestellt werden können, um so Raum für einen möglichen Quantenvorteil zu schaffen.

 

Full Configuration Interaction und die Superposition von Qubits

Die Full Configuration Interaction (FCI) ist eine Post-Hartree-Fock Methode und versucht den Grundzustand der Schrödinger-Gleichung aus der Überlagerung aller möglichen validen (dem Pauli-Prinzip entsprechenden) Konfigurationen der in der Hartree-Fock berechneten Molekülorbitalen zu konstruieren. Für das Beispiel von zwei Molekülorbitalen kann dies in der Dirac-Schreibweise mathematisch als eine lineare Kombination, oder Superposition, dargestellt werden,
c0|↓↑,□□> + c1|↓□,↓□> + c2|↓□,□↑> + c3|□↑,↓□> + c4|□↑,□↑> + c5|□□,↓↑> .
Die Koeffizienten ci beschreiben den Anteil der verschiedenen Konfigurationen zum Gesamtzustand. Zur Erinnerung: im Hartree-Fock-Grundzustand war Zustand durch die erste Konfiguration, |↓↑□□) , gegeben. In der FCI-Methode optimiert man die Koeffizienten sodass eine Lösung mit niedrigster Energie gefunden wird.

Mit Hilfe der Dirac-Schreibweise geben wir an ob ein Molekülorbital inklusive Spin-Freiheitsgrad besetzt oder unbesetzt ist. Dies können wir auch binär, also mit 0 (unbesetzt) und 1 (besetzt), darstellen. Für den Hartree-Fock-Grundzustand , |↓↑□□) können wir also |1100) schreiben und die obige Superposition der verschiedenen Konfigurationen können wir als
c0 |1100> + c1 |1010> + c2 |1001> + c3 |0110> + c4 |0101> + c5 |0011>
abbilden. Auf einem Quantencomputer können wir diesen Zustand mit Hilfe von vier Qubits darstellen, bei dem jedes Qubit anzeigt ob ein bestimmtes Molekülorbital inklusive Spin besetzt oder unbesetzt ist. Die Superposition der verschiedenen Konfigurationen kann dann also durch eine Superposition von Qubits dargestellt werden – der Paradedisziplin eines Quantencomputers!

Literatur:

[1] Bela Bauer, Sergey Bravyi, Mario Motta, and Garnet Kin-Lic Chan. Quantum algorithms for quantum chemistry and quantum materials science. Chemical Reviews, 120(22):12685– 12717, 2020.

[2] Yudong Cao, Jonathan Romero, Jonathan P Olson, Matthias Degroote, Peter D Johnson, M´aria Kieferov´a, Ian D Kivlichan, Tim Menke, Borja Peropadre, Nicolas PD Sawaya, et al. Quantum chemistry in the age of quantum computing. Chemical reviews, 119(19):10856– 10915, 2019.

[3] Qiming Sun, Timothy C Berkelbach, Nick S Blunt, George H Booth, Sheng Guo, Zhendong Li, Junzi Liu, James D McClain, Elvira R Sayfutyarova, Sandeep Sharma, et al. PySCF: the python-based simulations of chemistry framework. Wiley Interdisciplinary Reviews: Computational Molecular Science, 8(1):e1340, 2018.

[4] Richard P Feynman. Simulating physics with computers. International Journal of Theoretical Physics, 21:467–488, 1982.

[5] Wikimedia Commons. Different p-orbitals and s-orbitals. https://commons.wikimedia.org/wiki/File:AOs-1s-2pz.png, 2006. [Online; accessed 21-July-2012].

[6] David J Griffiths and Darrell F Schroeter. Introduction to quantum mechanics. Cambridge University Press, 2018.

[7] Attila Szabo and Neil S Ostlund. Modern quantum chemistry: introduction to advanced electronic structure theory. Courier Corporation, 2012.

[8] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J Love, Al´an Aspuru-Guzik, and Jeremy L O’brien. A variational eigenvalue solver on a photonic quantum processor. Nature communications, 5(1):1–7, 2014.

[9] A Yu Kitaev. Quantum measurements and the abelian stabilizer problem. arXiv preprint quant-ph/9511026, 1995.

[10] Michael A Nielsen and Isaac Chuang. Quantum computation and quantum information, 2002.

[11] Abhinav Kandala, Antonio Mezzacapo, Kristan Temme, Maika Takita, Markus Brink, Jerry M Chow, and Jay M Gambetta. Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets. Nature, 549(7671):242–246, 2017.

[12] Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C Bardin, Rami Barends, Sergio Boixo, Michael Broughton, Bob B Buckley, David A Buell, et al. Hartree-fock on a superconducting qubit quantum computer. Science, 369(6507):1084–1089, 2020.