1.Quantum Use Case Identification

With quantum computers (QC) on the rise to be the next powerful calculation accelerator, a new era to utilize and solve complex challenges is dawning. Learning from the past, where most companies began their way into the AI world way too late, it is time to start the journey into the quantum computing realm and the best way is learning by doing. Hence, one may refer the selection and evaluation process of a quantum computing use case longlist as a key milestone and the first ingredient to be the active force to shape it.

Employees represent an invaluable treasure of implicit and explicit knowledge of the inner workings and values of a company. Mining already existing ideas is in most cases a suitable and recommended approach to find the first set of use cases to further assess in a fail-fast approach. This approach might be even enhanced when it comes to identifying QC use cases, yielding only those use cases that are hidden in the sweet spot for a successful quantum computational implementation.

Quantum computing is still a new, very fast developing field. There are no widely accepted standards and the lack of experience when it comes to implementation is still a hurdle to take. This makes the selection process for pilot candidates very cumbersome. After business stakeholders, IT and quantum computing experts have compiled a longlist of use cases (incl. impact and currently limiting computing resources) to be evaluated, the very start for each identified use case is to formulate the problem statement and transform them into mathematical models. This article then proposes an approach to assess and select use cases with high feasibility based on computational complexity theory and technology limitations and prospects aware implementations. This approach relies on the application of a sequence of three sieves to peel away scenarios and use cases that would lead to a huge invest in resource and time without any promising outcome. Thus, leaving only the very core of the longlist which may yield substantial benefits through usage of quantum computers. Those three steps (depicted in Figure 1) consist of checking whether the model used to describe the use case can be solved efficiently on a QC, then checking available QC algorithms, always assessing if there are classical solutions that might be faster and finally making use of a checklist to avoid pitfalls and showstoppers when it comes to tool selection and implementation.

After applying all three sieves the initial set of use cases might have diminished heavily, as well as the risk of failure, before starting the phase of implementation and thus reflect an essence needed for a successful QC journey.

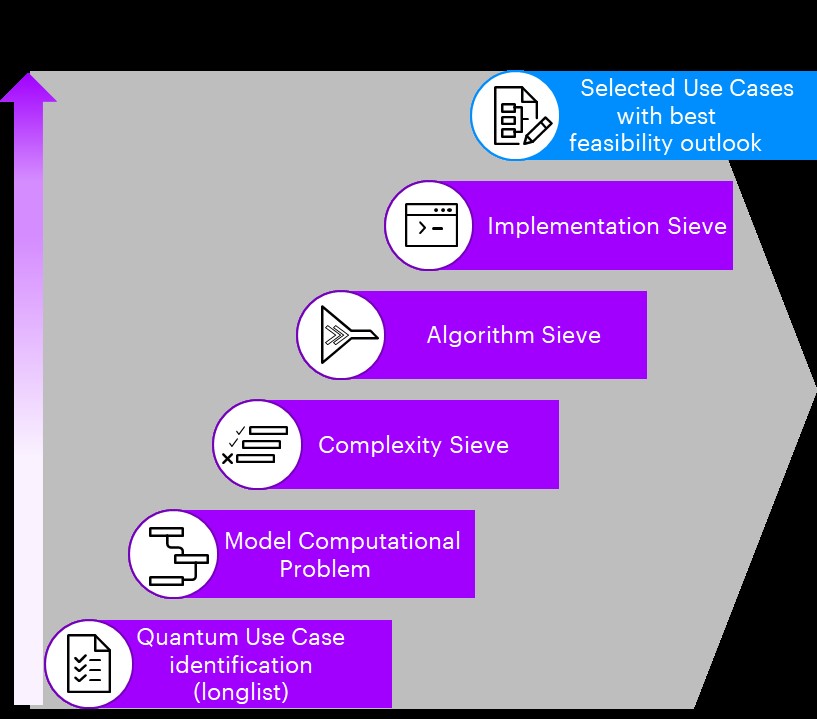
2. Model Computational Problem

Based on the informal descriptions of potential use cases from the previous ideation activities, the goal of this step is to precisely, in the sense of mathematical rigor, model and formulate the problem statement either in a mathematical notation (e.g. as common for mathematical programming or algebraic specification),  specification languages (e.g. AMPL [Fourer 2003]) or for more complex situations (esp. if (meta)heuristics are applied) to write evaluation functions for feasible/ optimal solutions in any general-purpose programming language. All these approaches add benefit over a pure informal use case description. Most importantly, precise modeling of input and output variables, the domain, co-domain and range of the problem as well as the definition of feasible (or optimal) solutions is mandatory for the subsequent steps. The model choice is a challenging task of describing a process or system sufficiently and efficiently, but out of scope of this QC specific approach. As will be detailed below, even minor changes in the problem’s description can change its characteristic properties, might even make it computationally intractable and thus render it infeasible as a quantum computing proof-of-concept (PoC) candidate. ­

The next section introduces concepts to formalize and analyze these kinds of (in)tractability.

3. The Complexity Sieve

Assume for a given problem a classical computer (CC) and QC would yield similar results in terms of required clock runtime. Should the associated use case then be implemented on a CC or QC? Naturally, a CC implementation is preferable, simply as software libraries and environments, the entire development process and especially the hardware is much more mature. This step’s objective (as well as those of the following) is to sieve out computational problems, and hence use cases, that potentially could be better solved by a CC.

3.1 Complexity Theory: Limitations & Opportunities of Computability

Over the last decades, computers became a ubiquitous tool to support human analysts and decision-makers in virtually all optimization and learning tasks. More precisely, software algorithms leverage the enormous and continuously increasing computing power of modern hardware – from Zuse’s Z3, a single 8-core laptop, over supercomputers and distributed computing nodes to the new kid on the block: quantum computers (QC). But can computers solve any problem?

This question emerged already in the early days of computing in the 1930s. It all started with the seemingly simple challenge to define what a computing problem is and consequently which of these problems a computer can solve. The result of this thought process, called the Church-Turing thesis, is the assumption – not provable but commonly accepted in the sense of an axiom – that in layman’s terms every (practical) computer irrespective of the type or architecture can solve exactly the same set of problems, namely the same problems that a human being can solve with pen & paper. Put differently, computers, including QCs, are in general not better (or worse) in problem-solving than humans, but of course extraordinarily faster. The obvious follow-up question is which computing problems a human (and hence a computer) can solve, which not and if there are categories of problems that are more difficult, or even intractable, to solve than others. The short answer is yes, there are multiple categories, called (computational) complexity classes, that exhibit different levels of difficultness, or (computational) complexity. Complexity classes exist for multiple kinds of computational resources, e.g. computation time, memory space and messages exchanged between communicating network nodes. This article is restricted to the predominantly limiting resource, time.

The legitimate question may arise why this step is required at all? Isn’t it more straightforward to directly jump into the solution part? No question, this shortcut would be possible. However, then you will miss important information and hints on where to look for a solution, and what kind of benefit you could expect from a quantum algorithm. What could be more frustrating than realizing after investing a significant amount resources that for this particular task a well-known classical algorithm solves the problem similarly well or that a quantum computer is even not much of a help per se? So, let’s start the adventurous journey into what Computer Scientists and Mathematicians call computational complexity theory.

Back to the initial question: can computers solve every problem? Astonishingly, the most complex problems are not solvable at all – neither by a human, nor any kind of computer, it is a general limitation of computability. The best-known representative is the famous Halting Problem [Arora 2007], i.e. the binary question: will a given computer program ever terminate? There is no (nor will there be) a general way to decide this seemingly simple question for general formal languages (any typical programming language falls into this category), hence this question is undecidable. Practical consequence: compilers will never have a built-in feature that will notify the user without fail that the project’s source code contains parts that might run in an infinite loop.So, as a first result: if the considered problem is not decidable, it is not worth looking any further. No computer, not even a QC, will help you. Fortunately, such problems do not occur too frequently in practice.

The insights complexity theory could contribute do not stop here. The excurse box 1 introduces additional basic concepts of classical complexity theory, the excurse box 2 extends this to the quantum world.

3.2 Applying the Sieve

Usually, a problem is not entirely new and thus already well evaluated in the literature (in the rare exceptions a thorough problem analysis is required which is beyond scope). Consequently, literature research using the formal problem specification derived in the previous activity, typically easily reveals the computational complexity as well as the pertinent algorithms. The following distinction is practically relevant (cf. the excurse boxes on complexity theory for an explanation of the relevant terms):

1. Classically Tractable Problems [𝑃, 𝐵𝑃𝑃 (and 𝐹𝑃,𝑃𝑂)]:: The problem is efficiently solvable by CCs and QCs (as 𝑃⊆𝐵𝑃𝑃⊆𝐵𝑄𝑃). Whether a quantum algorithm is still beneficial depends on the specific speed-up. For instance, the shortest path problem [Cormen 2001] is in P and efficiently solvable in theory and practice, a quantum implementation may not bring tangible improvements (esp. as no performant quantum algorithm is known for this problem). In contrast, the problem solved by the Grover algorithm, searching in an unsorted database with n elements (or more precisely a special version of function inversion) is also in P, classically with a linear time complexity with n steps in the worst case, can be solved in √𝑛 steps. Depending on the specifics of the problem at hand, this might be a relevant speed-up if the use case hits limits on a CC.

If the related use case is not limited by actual resource constraints on CCs such a problem is not a (high priority) quantum PoC use case candidate.

2. Potentially Classically Intractable Problems [from 𝑁𝑃 (and 𝐹𝑁𝑂,𝑁𝑃𝑂)]: Since the class NP is not (entirely) in  (analogously for related classes and problem sets) multiple subsets need to be evaluated individually.
   • NP-intermediate (and 𝐹𝑁𝑂-/𝑁𝑃𝑂-intermediate): The problem is not efficiently solvable by a CC, however some successful quantum algorithms for this set exist. One of the most prominent precedent cases for quantum computing falls in this category: Integer/ Prime Factorization by Shor’s algorithm [Arora 2007].

A prime PoC candidate.

• 𝑵𝑷𝑪, 𝑵𝑷-hard: The problem is not efficiently solvable by a CC. Unfortunately, these classes are conjectured to also not be in BQP, hence, the problem can likely (if 𝑃≠𝑁𝑃) not be solved by a QC in an exact and efficient way. Consequently, there cannot be an efficient quantum algorithm, however, a special kind of algorithms called metaheuristics can be used by CCs and QCs to possible find imperfect solutions. Note that if the problem is not in one of the next classes at the same time, approximations could get basically arbitrarily bad (the clique problem [Cormen 2001] is such an example).

If approximated solutions are acceptable, it is a PoC candidate.

• 𝑨𝑷𝑿,𝑷𝑻𝑨𝑺: The 𝑁𝑃𝑂 problem is efficiently approximable by a CC but might exponentially depend on the specified maximum admissible error. An example for 𝐴𝑃𝑋 is the notoriously difficult (metrical) Traveling Salesman Problem (TSP [Cormen 2001]) and the m-dimensional Knapsack [Cormen 2001] problem has even a 𝑃𝑇𝐴𝑆.

If approximated solutions are acceptable, it is a PoC candidate.

• 𝑭𝑷𝑻𝑨𝑺: The 𝑁𝑃𝑂 problem is efficiently approximable on classical computers irrespective of the admissible error. Popular examples include the Bin Packing problem [Cormen 2001] and the 1-dimensional Knapsack problem (apparently another instance where changes in the problem formulation can lead to significant complexity changes).

Thus, the same considerations as for class P apply.

3. Intractable Problems [Undecidable]: Could neither be solved by a classical nor by a quantum computer (cf. Halting Problem).

Trivially not a QC PoC candidate.

Applying this complexity sieve gives a first idea of the set of admissible use cases that could benefit from a quantum implementation.

4. Algorithm Sieve

The next step is to look up potential quantum algorithms in the literature based on the formal problem description. This activity could yield the following results:

1. Perfect fit: In the simplest case, a perfectly fitting quantum algorithm is already known and can be immediately applied to the problem. Compared to the virtually uncountable number of classical algorithms, the number of known quantum algorithms is significantly lower. Alas, chances are that a precisely fitting algorithm has not yet been discovered (or does not exist). A valuable resource for a quantum algorithm overview and finding potential candidate algorithms is [QAZ 2021].
2. Transformation required: As the number of discovered quantum algorithms is comparatively low, it is more likely that algorithms for related problem areas exist. It is therefore not uncommon that it is required to transform an input instance of the problem at hand into input instances of the related problem for which quantum algorithms exist and finally to transform back the output (the polynomial reductions applied in complexity theory could serve as an inspiration). Practically, in case efficient (esp. linear) transformations are available both problems can be considered equal and are just differently formulated.
3. Approximation / Metaheuristic applicable: In case no efficient exact algorithm is available and classical (meta)heuristics do not lead to the expected success, quantum approximation algorithms for specific problems or general metaheuristics for broader classes of (combinatorial) optimization/search problems might help. Examples of widely used quantum metaheuristics are Quantum Annealing (QA) [Kadowaki 1998] and Quantum Approximate Optimization Algorithm (QAOA) [Farhi 2014]. If such algorithms are applied, it is a priori compulsory to precisely define the admissible error and to understand the algorithm’s potential solution guarantees in advance.
4. No applicable algorithm found: If no quantum algorithm exists or a transformation is too complicated, obviously, the use case is not a PoC candidate.

Assuming an efficient quantum algorithm has been identified, the subsequent step is to compare its computational complexity with classical counterparts revealed during literature research. Two aspects then play an important role:

1. Runtime complexity: For exact algorithms, the key metric is the (asymptotical) growth of the required computational steps as a function in the number of input units. In the algorithmic literature it is commonly provided in the Big O notation [Cormen 2001] that abstracts away large coefficient constants prolonging the runtime multiplicatively. Where these constant factors are predominant runtime determinants it is usually stated explicitly in the literature.
2. Convergence complexity: For approximation algorithms and (meta)heuristics, the key metric is the number of steps required to reach a certain level of approximation quality (also provided in Big O notation). Especially for metaheuristics, however, empirical analyses for are typically more insightful.

As QCs are conceptually not faster than CCs but draw all their strength from algorithmic speed-ups opportunities provided by the underlying quantum mechanical peculiarities, a quantum algorithm should be at least super-linearly, or even quadratically, better (in runtime or convergence) in order to be considered realistically superior. Otherwise the next generation of supercomputers or massively distributed computing nodes, might be able to provide solutions faster and cheaper.

Problems solvable by such superior quantum algorithms, also pass this second sieve successfully and flow into the third sieve that filters for hurdles of existing tooling for hardware and algorithms.

5. Implementation Sieve

The international race to exploit the abstract space of quantum mechanics (“Hilbert-space”) drives rapid developments of the hardware and algorithms. In order to assess the use case’s recent and perspective success probability the implementation feasibility sieve points out applied measures and pitfalls by reviewing common algorithm assumptions on hardware capabilities and limitations, as well as mitigation methods.

A general hardware-agnostic check regards the problem models structure:  As one example quantum machine learning (QML) algorithms rely on sparsity (number of entries in a matrix) [Biamonte 2016] and thus exclude large fractions of instances. Further the sizable impact of instance structures on performance of QML has been shown by [Huang 2020].

The hardware-aware assessment depends on the choice of the model of quantum computer and it’s bridge technologies, which soften the entry barrier to post-quantum:

1. von-Neumann Computers (CPU + Memory) or Accelerators/Co-Processors – Developments in quantum technology also spark ideas in related fields. The development of algorithms, created to solve problems in similar ways as quantum algorithms sometimes called quantum inspired algorithms (e.g., recommendation systems [Tang 2018], optimization [Zhu 2016]) also drive developments in creating application specific hardware. Although these types of algorithms run on classical CPU or accelerators like graphic cards (GPU) used in production today, even faster field programmable gate arrays (FPGA) and application specific integrated circuits (ASIC), or quantum-inspired digital technology has been developed, that can perform parallel, real-time optimization calculations with improvements in the percent range [Castellanos 2020] compared to the companies best practice. The success of this technology will rely on scaling faster, than competitors as the small performance advantages typically vanish with the next revision cycle.
2. Quantum annealers – can be employed for optimization or simulation tasks and offer to represent problems with dozens of binary variables already today, using quantum effects to discover better solutions within the very-short lifetime of these effects (ca. one-millionth of a second) with debated practical potential as it is a heuristic approach with reduced generality. These machines offer a learning and development platform for small scale (dozens of variables) problems and PoC today.
3. Gate quantum computers – use the full theoretical potential of quantum effects and enable 1000x longer calculation times at the cost of reduced number of qubits (50-100) to represent variables. These machines were the first proving advantage for the previously mentioned highly specialized problems related to quantum physics questions (solving these problems in minutes compared to thousands of years), small scale optimization [Arute 2019], chemistry [Nam 2019]. The latter team announced they aim for quantum advantage – a drastic speed-up on a practical problem – within the next year.
4. Error-corrected (digital) quantum computers – use the full potential (e.g., decrypting types of secret messages within a day compared to millions of years for a CC) by algorithms to detect in the NISQ devices and correct them during calculation. Recent research gets closer, to realizing a long-lived (towards seconds) qubit called “logical qubit” of which a few thousands would be enough according to recent research results on hardware limitation aware runtime complexity to simulate previously intractable improved pricing for derivatives [Chakrabarti 2020] or cryptanalysis based on prime factorization [BSI 2018].
5. Analogue quantum computers/ quantum simulators leverage the continuous control of for example ultracold atoms in optical traps and are used in fundamental research to simulate complex electronic structures for material science.

Depending on the scope of the use case we advise to decide on these core hardware platforms intermediate implementations that meets the requirements. Keep in mind that today`s noisy intermediate scale quantum computers (NISQ) (types 2-5) use different physical systems to represent the qubits with impact on main performance indicators like maximum number of qubits, number of gates executed before errors dominate the process and interconnections as well as the universality of operations (e.g., quantum annealers are limited in generality regarding the simulation of quantum systems). The following exemplary list extends features to check to filter infeasible use case, with further “hardware-efficient” approaches listed in [Bharti 2021]:

1. Preprocessing – The solution of problem instances on quantum computers relies on mapping binary variables on qubits and dependencies on interactions between them, thus the topology of the problem needs to be embedded on that of the QC. These embeddings are generally NP-hard it is important to identify problem structure classes that respect the widely varying connectivity graphs of different QC implementations (e.g., superconducting, ion-trap or photonic QCs) or check leading heuristics performance.
2. State Preparation – the efficient preparation of an initial state can be a bottleneck of the algorithm as a QC always starts in the all-0-state. Domain specific efficient representations or machine learning methods black box to optimize the state initialization have been developed for some cases. Additionally, a family of algorithms assumes a quantum computer module called “QRAM” – a long-lived quantum random access memory – that is not expected by the scientific community anytime soon and is a prerequisite of e.g., QML algorithms like HHL. Applications relying on these algorithms are not feasible in the near future.
3. Unitary Transformation – exact algorithms (Grover) with quadratic speed-ups are likely to be overthrown by the error-correction overhead for the near future [Babbush 2020]. Additionally, “native gate sets” – additional instruction sets available for a QC that resemble problem or hardware native operations (e.g., the exchange of electrons in a molecule) impact the algorithm complexity.
4. Measurement – determining the output of a quantum calculation resets the complex quantum state to a classical state. All quantum algorithm concepts take this behavior into account, but hybrid algorithms involving iterations of a loop of quantum circuits, measurements and updates to the circuits by classical computers can be limited by the amount of iterations given by the number of measurements. Algorithms that leverage recent approaches can reduce the number of measurements by 90% [Verteletskyi 2020], [Sweke 2020] increase the implementation feasibility on today`s hardware.
5. Postprocessing – for variational methods’ the duration of the iterative loop of evaluating the quantum circuit result and then updating the hyperparameters to configure the next circuit is critical. Thus, choosing an approach that compiles new circuits at low latency with gradient-based or gradient-free approaches, as well as a hardware running the optimization-loop fast in direct proximity to the quantum chip at low latency is critical for edge use-case candidates’ speed-up.

Additionally, methods of „error mitigation” reduce the errors produced during the algorithm steps can reduce complexity. For approximative algorithms, it is important to review if the use case critical algorithm can represent a rich class of quantum states and thus possible solutions (expressibility), if these states can be created at algorithm runtime (reachability) and if the initial solution quality can be improved (trainability). Checking for recent results regarding the algorithm can exclude use cases that require short implementation time scales and build the basis of the following step of technical solution design, which is out of scope of this article.

6. Summary

For many companies, the first steps on their own quantum computing journey have yet to be taken.

It is recommended to define an outcome (e.g., showcase, training platform, proof-of-concept, prototype) specific requirements analysis and solution blueprint (e.g., framework choice, coding guidelines, cloud architecture, tooling support incl. CI/CD pipeline) for future reference alongside the implementation based on the experiences. The complexity theory-backed method described in this article may help to select and assess use cases to allocate budget in a reasonable way. Even though a huge part of initial ideas might drop in the process and only a handful remain to be viable, there is no doubt that QC will play a key role within the future IT architectures. Moreover, as first mover advantage one may shape industry standards for quantum computing and directs design or research on new algorithms into the directions of one’s own needs.

Excurse Box 1: Classical Complexity Theory

In a complexity theoretical context, it is necessary to discriminate several variants of computational problems: 1. Decision problem: A problem that can be answered by yes or no. The aforementioned Halting Problem is exactly such a decision problem. Another example is the question: “Does a path between these two cities exist with at most  cost units?” 2. Function problem: An extension of the decision problem in the sense that a single output per input is generated but where the output can be more complex than just yes/no. For instance, for the question “What is a path between these two cities with at most x cost units?” a path (sequence of graph edges) is requested. 3. Optimization problem: A problem which has potentially multiple feasible answers, each associated with a cost value, where the answer with the best cost (minimum or maximum, depending on the use case) is the searched optimal value. An example: “What is the cost of the shortest path between these two cities?” 4. Search problem: A variant of the optimization problem asking for the actual solution that leads to the optimal cost value, e.g. the path with the minimal cost. By clever encoding, the search problem can be solved using the optimization variant for many problems and, thus, for the scope of this discussion, the first can be treated as a special case of the latter and will be neglected in the following description. Complexity theory [Arora 2007] mostly focuses on the decision versions as a binary answer simplifies theory and already allows for providing (lower) bounds also for the other variants. A simplified overview of the relevant classes of the complexity landscape can be found in Figure 2. 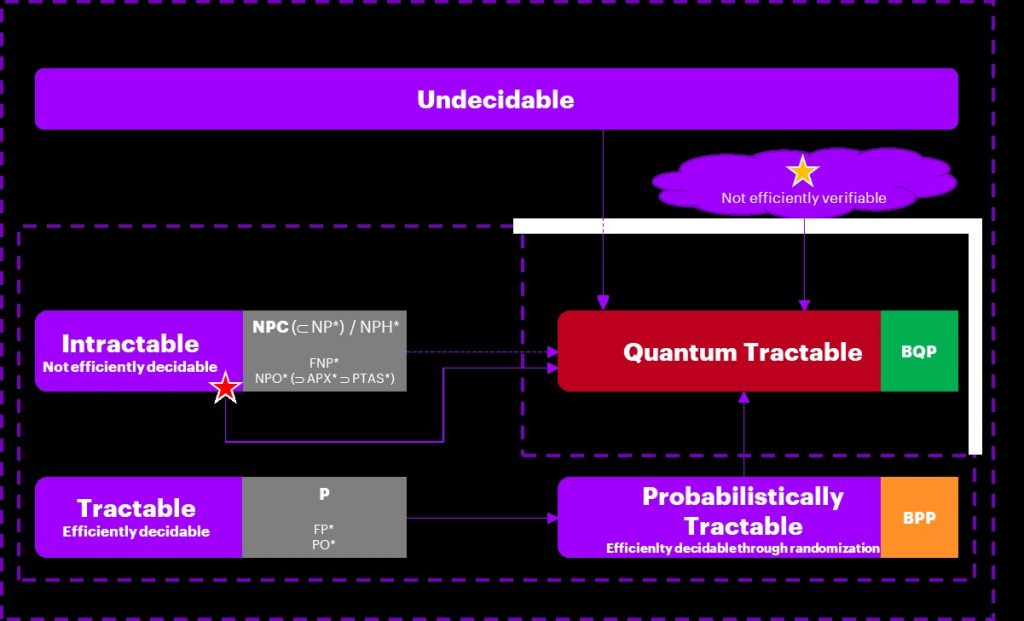Many, if not most, of the problems that one encounters in the wild belong to a complexity class that is part of the so-called Polynomial Time Hierarchy (𝑃𝐻). It encompasses decision problems for which a given solution could be verified to be valid (a yes (no) instance yields a yes (no)) such that the number of computational steps of the verification process is polynomially bounded in the size of the input (e.g. the edges and nodes in a graph for a shortest path problem). The complexity theory is inclined to consider such polynomial upper bounds in 𝑛 inputs, i.e. all functions that do not grow faster than (n^c) for any constant c , typically noted as 𝑂((n^c)) in the so-called Big O notation [Cormen 2001], as efficient (cf. Cobham’s thesis [Cobham 1970]). This is based on the underlying notion that such computations are typically still tractable on practical hardware in the sense of acceptable (clock) runtime. In contrast to super-polynomial, esp. exponential, growth, that could quickly lead to computations taking millions of years for even moderate input sizes using any foreseeable computer technology. Using this terminology, all problems in 𝑃𝐻 are efficiently verifiable as it is guaranteed that at least one polynomial verification algorithm exists. Unfortunately, an efficient verification, however, does not necessarily imply that deriving a solution is efficiently calculatable (and hence might require a super-polynomial time algorithm, e.g. with exponential growth). Moreover, it is also true that Cobham’s thesis is just a rule of thumb, but a practically good one. There are examples of algorithms that are efficient by this definition but their runtime is dependent on large coefficients or the number of required inputs is so large that cubic (c=3) or even quadratic (c=2) polynomial degrees could already lead to computations taking too long for some real-world use cases. However, often, the runtime’s growth dependency on the input size is a good estimate so that the knowledge of the inherently minimal possible complexity of a problem as well as the runtime guarantees of the candidate algorithms are invaluable. The simplest class in 𝑃𝐻 depicted in the diagram is called 𝑃 (for Polynomial Time). As the name implies, it contains all decision problems for which efficient decidability has been proved. Consequently, these decision problems are typically easily decidable in the sense that the computational requirements are comparatively low even for large input sizes. In other words, a CC can usually quickly decide if the input is a yes instance. But does this help us in the assessment of the considered problem, which is usually rather an optimization problem than a decision problem? The answer is clearly positive: 1. A decision version is always a lower bound in terms of time complexity for the related function and optimization version. In other words: finding an optimal or even any solution cannot be simpler than the decision variant. 2. In many cases, the function, optimization and search problem is efficiently solvable if the decision problem is efficiently decidable (if the decision problem can be used as an oracle function at most polynomial times to solve the function or optimization problem). The shortest path problem might serve as an example: the decision problem is in 𝑃 and indeed the function, optimization and search problem, i.e. getting actually the shortest path and the associated cost, can be solved in polynomial time (in the number of cities) as well (e.g. by application of the Dijkstra algorithm [Cormen 2001]). Consequently, these problem variants are part of other polynomial classes, namely 𝐹𝑃 (Function Polynomial) and 𝑃𝑂 (Polynomial Optimization) for the function and optimization problem, respectively. Naturally, not all problems in the world can be easily solved. In complexity theory, many different levels of difficultness are known. To understand this better, let’s first review the underlying concepts of computational models. Theoretical computer science in general and complexity theory in particular requires a formal computing model to abstract away all the constantly changing details of actual hardware. Alan Turing, the famous English code breaker and mathematician, introduced such a theoretical model, now named Turing Machine in honor of him, in the late 1930s. It is a very minimal, but due to its infinite memory, purely fictional abstract machine that, despite its simplicity, is still equivalent to (all) real computers in terms of accomplishable tasks in the sense of the Church-Turing thesis described above. This model always starts in a single state, then executes a single action and subsequently transitions into a resulting new single state and repeats this process until a stop criterion is reached. As the sequence of steps (state 0 -> action 0 -> state 1 -> …) forms a computational path that is always the same for a given initial state, the model is more precisely known as Deterministic Turing Machine (DTM). DTMs constitute the class , i.e. they can efficiently decide exactly those problems in . Now imagine an at first glance much more powerful extension. Instead of a single state-action-state transition, the model branches in all possible subsequent states concurrently by executing every action possible at once, hence forming a computational tree. Such a, obviously purely theoretical, model is known as Non-deterministic Turing Machine (NTM). It is the missing link between efficiently and non-efficiently decidable problems. An NTM constitutes the class  (Non-deterministic Polynomial) which is the set of decision problems polynomially decidable by an NTM. As a DTM is a special case of an NTM, the class  is trivially a superset of . But is this also true the other way around? This is the most famous open question in computer science and an introductory description of complexity theory is of course not complete without a reference to it: does equal 𝑃 equal 𝑁𝑃 (𝑃=𝑁𝑃)? It might come as a surprise, but the seemingly magical NTM is not more powerful than a plain DTM regarding the set of computable tasks. If a problem is computable by an NTM it can also be computed by a DTM. It is conjectured, but not yet proven, however, that this is not possible in a polynomial number of steps. Effectively. this means that likely problems in  exist that are efficiently decidable by an NTM but not by a DTM, hence 𝑃≠𝑁𝑃. The practical relevance attached to it is that CCs, which basically resemble DTMs with finite memory, are therefore (likely) not capable of efficiently deciding all problems in 𝑁𝑃. The most interesting subset of 𝑁𝑃, which only contains decision problems that a DTM could decide in super-polynomial time (i.e. inefficiently), is called 𝑁𝑃𝐶 (NP Complete). Informally, these problems are also known as the most difficult problems in 𝑁𝑃. All decision problems in 𝑁𝑃𝐶 have the fascinating characteristic that they are complete for the entire class 𝑁𝑃, in the sense that an algorithm A that decides such an 𝑁𝑃-complete problem can also be used to decide all other problems in 𝑁𝑃 as well. The trick is to turn the input instances into input instances of algorithm A using a polynomial-time transformation and to revert the output. This technique is called (polynomial) reduction: all problems in 𝑁𝑃 are reducible to any 𝑁𝑃-complete problem. Closely related to 𝑁𝑃𝐶 are problems that are at least as hard as any 𝑁𝑃𝐶 problem, but not necessarily are in 𝑁𝑃. These problems are called 𝑁𝑃-hard and are not restricted to decision problems (e.g. the famous optimization problem Traveling Salesman Problem (TSP) is 𝑁𝑃-hard). The concept of reductions also leads to a strong argument in favor of 𝑃≠𝑁𝑃: Once just a single efficient algorithm would have been found for a 𝑁𝑃-complete or 𝑁𝑃-hard problem, all problems in NP would be decidable in polynomial time. As this has not yet happened in the last decades, many complexity theorists consider it as mounting evidence that there is none. In summary, 𝑁𝑃 contains efficiently (subset 𝑃) and (likely) non-efficiently (subset 𝑁𝑃𝐶 and others) decidable problems by a classical computer. Hence, not all problems are solvable quickly but, as 𝑁𝑃 is in 𝑃𝐻, candidate solutions for all decision problems in NP are at least efficiently verifiable. Analogously to 𝐹𝑃 and 𝑃𝑂, the class 𝐹𝑁𝑃 (Function 𝑁𝑃) and 𝑁𝑃𝑂 (𝑁𝑃 Optimization) are defined for function and optimization problems, respectively. So far, we have only discussed algorithms that solve problems always exactly, or deterministically. Two alternatives exist: 1. Probabilistic algorithms: The computing models analyzed so far are entirely predictable: a DTM and NTM cannot roll a dice and thus gives seemingly away a lot of algorithmic potential. The classical example of a complexity class taking randomness into account is 𝐵𝑃𝑃 (Bounded-Error Probabilistic Polynomial), intuitively the set of problems efficiently decidable by probabilistic algorithms. The obvious downside of such randomization is that they might not always generate correct answers. However, as long as they are correct in at least half of the cases, multiple executions of the algorithm lead to (almost arbitrarily) higher confidence, a technique called probability amplification. As DTM algorithms always generate the same output, 𝑃 is trivially a subset of 𝐵𝑃𝑃. Astonishingly enough, although randomized algorithms have more degrees of freedom, it is conjectured that it might not lead to a larger set of efficiently decidable problems (𝑃=𝐵𝑃𝑃?). It is worth noting that randomization is not the same concept as the non-determinism of an NTM: the action of a probabilistic algorithm might be based on a coin flip but it still transitions into a single next state, not concurrently into multiple states. Probabilistic extensions of NP tough exist (e.g. so-called Merlin-Arthur games, class 𝑀𝐴) but are beyond the scope of this article. 2. Approximation algorithms: Another alternative approach is to accept inferior solutions to optimization and search problems. In the infamously complex Traveling Salesman Problem (TSP) the objective is to find a minimal cost loop (starting and ending in the same city) that visits all cities. It is an example of an 𝑁𝑃-hard problem, an exact solution cannot be computed efficiently on any computer. But is an optimal solution in all cases required? As long as the error is small enough, it might be an acceptable trade-off to calculate a path that is slightly longer but to get the result quickly (compared to waiting thousands of years just to save a few minutes en route). Turns out that several kinds of approximability exist. The most general one in 𝑁𝑃𝑂 is called 𝐴𝑃𝑋 (Approximable): it is the set of 𝑁𝑃𝑂 problems for which polynomial-time approximations algorithms exist such that the error is multiplicatively bounded by a constant 𝑐, i.e. the worst value is less than 𝑐𝑣∗, for 𝑣∗ being the optimal value. In simple terms, an efficient approximation algorithm exists and the (relative) error is bounded (and hence does not depend on the size of the input) but 𝑐 may get arbitrarily large. A better guarantee can be provided for optimization problems that have a 𝑃𝑇𝐴𝑆 (Polynomial Time Approximation Scheme). For these problems, algorithms exist which can calculate arbitrarily good approximations polynomial in the input size but could be super-polynomial in the admissible (but fixed) error [latex]varepsilon[/latex]. 𝑃𝑇𝐴𝑆 usually depend exponentially on [latex]1/varepsilon[/latex] and hence might take exponentially longer if a smaller error is chosen. The strongest guarantee is found in problems that have an 𝐹𝑃𝑇𝐴𝑆 (Fully PTAS), where the algorithm also needs to be polynomial in [latex]varepsilon_1[/latex], and hence can efficiently approximate the problem for any given error. To cut the long story of classical complexity short, problems can be categorized into classes that characterize their general solvability: exact and efficiently (𝑃; 𝐹𝑃; 𝑃𝑂), exact and inefficiently (𝑁𝑃𝐶,𝑁𝑃𝐻;𝐹𝑁𝑃;𝑁𝑃𝑂), probabilistically exact and efficient (BPP), efficiently approximable (𝐴𝑃𝑋,𝑃𝑇𝐴𝑆,𝐹𝑃𝑇𝐴𝑆), and finally, not solvable at all.

Excurse Box 2: Quantum Complexity Theory

References

[Arora 2007] Arora, S., & Barak, B. (2007). Computational Complexity: A Modern Approach. Complexity.

[Arute 2019] Arute, F. et al.  (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574(7779), 505–510.

[Arute 1 2019] Arute et al. (2020). Quantum Approximate Optimization of Non-Planar Graph Problems on a Planar Superconducting Processor.

[Babbush 2020] Babbush, R. et al. Focus beyond quadratic speedups for error-corrected quantum advantage. arXiv (2020).

[Biamonte 2016] Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., & Lloyd, S. (2016). Quantum Machine Learning.

[BSI 2018] Office for Information Security, F. Status of quantum computer development (2018).

[Castellanos 2020] https://www.wsj.com/articles/microsofts-quantum-computing-services-attract-new-customers-11589900401

[Chakrabarti 2020] Chakrabarti, S. et al. (2020). A Threshold for Quantum Advantage in Derivative Pricing.

[Cormen 2001] Cormen, T. H., Leiserson, C. E., & Rivest, R. L. (2001). Introduction to Algorithms, Second Edition. In Computer

[Fourer 2003] Fourer, Robert, David M. Gay, and Brian W. Kernighan. AMPL: A Modeling Language for Mathematical Programming. 2nd ed. Pacific Grove, CA, 2003.

[Huang 2020] Huang, H.-Y. et al. Power of data in quantum machine learning. (2020).

[Leymann 2019] Leymann, F. Towards a Pattern Language for Quantum Algorithms. (2019).

[Leymann 2020] Leymann, F., & Barzen, J. The Bitter Truth About Quantum Algorithms in the NISQ Era. Quantum Science and Technology. (2020)

[Nam 2019] Nam, Y et al. (2019). A Ground-state energy estimation of the water molecule on a trapped ion quantum computer.

[Tang 2018] Tang, E. A quantum-inspired classical algorithm for recommendation systems. (2018)

[Zhu 2016] Zhu, Z. et al. borealis – A generalized global update algorithm for Boolean optimization problems. (2016)

[Cobham 1970] Cobham, A. (1970). The intrinsic computational difficulty of functions. Journal of Symbolic Logic, 34(4).

[Fourer 2002] Fourer, R., Gay, D. M., & Kernighan, B. W. (2002). AMPL: A Mathematical Programing Language.

[Kadowaki 1998] Kadowaki, T., & Nishimori, H. (1998). Quantum annealing in the transverse Ising model. Physical Review E – Statistical Physics, Plasmas, Fluids, and Related Interdisciplinary Topics.

[Farhi 2014] Farhi, E., Goldstone, J., & Gutmann, S. (2014). A Quantum Approximate Optimization Algorithm.

[Raz 2019] Raz, R., & Tal, A. (2019). Oracle separation of BQP and PH. Proceedings of the Annual ACM Symposium on Theory of Computing.

[QAZ 2021] Quantum Algorithm Zoo. Retrieved January 23, 2021, from https://quantumalgorithmzoo.org

[Sweke 2020] Conway, J., & Kochen, S. (2010). Thou Shalt Not Clone One Bit! Foundations of Physics, 40(4), 430–433

[Bharti 2021] Bharti, K. et al. (2021). Noisy intermediate-scale quantum (NISQ) algorithms