Abstract
Das Assignmentproblem ist ein fundamentales Optimierungsproblem mit vielen praktischen Anwendungen. Wir wollen aufzeigen, dass eine Lösung beliebiger Instanzen dieses Problems mit Quantum Annealing möglich ist und einen detaillierten Blick auf eine konkrete Anwendung werfen, die hierdurch in der industriellen Praxis optimiert werden kann.
Einleitung und Motivation
In vielen Bereichen der Forschung und der Industrie tun sich aktuell dank immer ausgereifteren und größeren Quantencomputern neue Möglichkeiten auf. Die Frage nach einer baldigen Quanten-Überlegenheit, also der Möglichkeit, mit einem Quantencomputer Probleme schneller oder genauer als mit einem klassischen System zu lösen, wird heiß diskutiert und durch neue Anwendungen, Technologien und Forschungsprojekte immer weiter befeuert.
Die Realität ist jedoch, dass die meisten, wenn nicht alle Quantentechnologien noch in den Kinderschuhen stecken. Mit Qubitzahlen im niedrigen zweistelligen Bereich, wie zum Beispiel bei IBM [1], lassen sich kaum Probleme nennenswerter Größe, gerade für die praktische Anwendung in der Industrie, angehen. Eine potenzielle Ausnahme bietet das Quantum Annealing, für das das Unternehmen D-Wave der Öffentlichkeit bereits Systeme mit mehreren Tausend Qubits zur Verfügung stellt. Diese Maschinen sind zwar keine universellen Computer, sondern arbeiten ausschließlich mit Optimierungsproblemen bestimmter Formate; die Firma selbst behauptet dafür allerdings, dass hiermit bereits einige industriell relevante Anwendungen besser gelöst werden können als mit klassischen Rechnern [2].
Eines der Probleme, die mit Quantum Annealing angegangen werden können, ist das Assignmentproblem. Dieses fundamentale Optimierungsproblem in einem gewichteten, bipartiten Graphen stellt die Frage nach einem Matching mit minimaler Summe der Kantengewichte im Matching. Das Assignmentproblem ist bereits gut erforscht und mit klassischen Methoden sowohl approxiermierbar als auch algorithmisch lösbar. Die bekannten Algorithmen, selbst für die Approximierung, haben allerdings erhebliche Laufzeiten für in der Industrie relevante große Probleminstanzen [3]. Zudem weicht die Qualität heuristischer Annäherungen von den Idealwerten oft in relevantem Maße ab. Sollten Lösungen, die Quantum Annealing nutzen, die Qualität der bekannten Heuristiken erreichen, könnten sie ein wichtiges Werkzeug für die praktische Anwendung werden und ein Schritt in Richtung der bereits erwähnten Quanten-Überlegenheit sein.
Wir befassen uns in diesem Beitrag genauer mit der Verwendung von Quantum Annealing zur Lösung des Assignmentproblems und einigen potenziellen Anwendungen, die sich in der Industrie daraus ergeben. Hierbei möchten wir die besprochenen Sachverhalte für den interessierten Leser ohne besondere Vorkenntnisse bezüglich Matchingproblemen oder Quantum Annealing verständlich machen.
Zunächst definieren wir das Assignmentproblem formal und gehen kurz auf bekannte klassische Algorithmen und insbesondere ihre Laufzeiten ein. Danach zeigen wir auf, dass dieses Problem nicht nur ein fundamentales Optimierungsproblem in der Wissenschaft ist, sondern auch wichtige Anwendungen in vielen Bereichen der Industrie hat. Als konkretes Beispiel betrachten wir die Planung einer global verteilten Supply Chain. Mithilfe einer Prognose der Nachfrage können wir einen Teil der Planung als Instanz des Assignmentproblems modellieren. Hierbei entspricht minimales Kantengewicht einer optimalen Einteilung der verfügbaren Produktionsmittel. Dieser Anwendung geben wir den Namen Demand-Supply-Matching. Anschließend führen wir das von D-Waves Quantum Annealern verwendete Format Quadratic Unconstrained Binary Optimization, kurz QUBO, ein und legen dar, wie man eine beliebige Instanz des Assignmentproblems in diese Form überführen kann, um es danach mit Quantum Annealing oder auch einer anderen Lösungsmethode für QUBO-Probleme behandeln zu können. Zuletzt versuchen wir uns an einem Ausblick auf weitere Anwendungsfälle und mögliche Methoden zur Verbesserung der Ergebnisse, die Quantum Annealing für das Assignmentproblem liefert.
Das Assignmentproblem
Das Assignmentproblem arbeitet auf einem gewichteten bipartiten Graphen (G= (V,E)). Das bedeutet, dass die Knotenmenge V in zwei disjunkte Teilmengen A und B partitioniert werden kann, sodass für jede Kante (e=(a,b)) gilt: (a ∈ A) und (b ∈ B) . Jeder Kante ( e ∈ E) wird ein Kantengewicht ( w_e ∈ R) zugeordnet. In diesem Graphen soll nun ein Matching, also eine Teilmenge ( M ⊆ E), in der für jede zwei Kanten ( m,n ∈ M) gilt, dass sie keinen Knoten teilen, gefunden werden. Dabei suchen wir dasjenige Matching, welches die Summe der Kantengewichte (sum _{m∈M}w_{m}) maximiert bzw. minimiert.
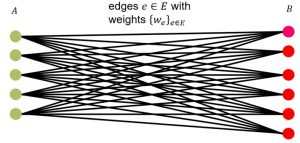
Duan und Pettie beschäftigten sich 2014 extensiv mit klassischen Methoden zur Lösung sowie zur Approximierung des Assignmentproblems und des allgemeineren Maximum Weight Matching-Problems. In ihrer Aufstellung finden sich Algorithmen, die das Assignmentproblem in (O(m√n+n^2 logn)) bzw. für ganzzahlige Kantengewichte in (O(m√n logN)) mit (m∶=|E|,n∶=|V|) und (N∶= max({w_e:e∈E})) lösen. Sie entwickelten außerdem einen Approximationsalgorithmus mit Laufzeit in (O(mϵ^{-1} logϵ^{-1})), wobei (e>0) als Betrag des maximalen Fehlers, den man in Kauf nimmt, definiert ist [3]. Alle diese Laufzeiten sind mindestens linear in (m) , also in der Anzahl der Kanten in (G), was bei einer großen Probleminstanz zu erheblichem Zeit- und Rechenaufwand führt. Quantum Annealing bietet hier die Chance, maßgeblich an Aufwand zu sparen, sofern es ebenfalls gute Ergebnisse liefert.
Erstes Anwendungsbeispiel: Supply Chain-Planung via Demand-Supply-Matching
Die Planung einer großen Supply Chain mit vielen, weltweit verteilten Produktionsstätten, und einer konstant fluktuierenden Nachfrage ist ein sehr komplexes Problem. Von dessen Optimierung hängen sowohl Gewinn als auch Kundenzufriedenheit maßgeblich ab. Im Folgenden wollen wir skizzieren, wie man durch die Lösung eines speziell konstruierten Assignmentproblems zumindest einen Teil dieser komplizierten Planung vereinfachen und dann auch optimieren kann.
Hierfür benötigen wir einen Überblick über die verfügbaren Produktionsstätten des betrachteten Unternehmens und ihre potenzielle Leistung für die betrachtete Zeitspanne (im folgenden Angebot genannt) sowie eine Vorhersage der angefragten Produktmengen in derselben Zeitspanne (im folgenden Nachfrage). Das verfügbare Angebot soll dann so genutzt werden, dass der erzielte Gewinn maximiert wird, indem die Nachfrage zu einem möglichst großen Teil abgedeckt wird. Wir treffen zwei vereinfachende Annahmen, die in der Praxis meistens gegeben sind oder durch eine Anpassung der Prognose der Nachfrage erfüllt werden können:
- Die Nachfrage lässt sich in einzelne Teilaufträge zerlegen, die nicht voneinander abhängen und ungefähr identische Ressourcen benötigen (z. B. die Fertigung einer bestimmten Stückzahl eines bestimmten Produkts).
- Das Angebot ist nie in der Lage, die Nachfrage komplett zu bedienen, ohne selbst voll ausgelastet zu sein.
Mit diesen Annahmen können wir nun zwei Mengen (S) und (D) definieren. (S) enthält ein Element für jeden Auftrag, den eine der Produktionsstätten in der betrachteten Zeitspanne ausführen kann. (D) enthält ein Element für jede auszuführende Tätigkeit in der Nachfrage. Diese beiden Mengen bilden unsere Knotenmenge (V=S ∪ D) für das Assignmentproblem. Wir definieren dann die Kantenmenge (E), indem wir eine Kante (e_{sd}) zwischen allen (s∈S) und (d∈D) einfügen, für die eine Zuweisung des Auftrags d) zur Produktionsstätte, der (s) zugeordnet ist, theoretisch möglich wäre. Wie genau dabei die Kantengewichte zu wählen sind, ist noch eine offene Frage bei dieser Anwendung, jedoch sollten sie offensichtlich den erzielten Umsatz durch die jeweiligen Zuweisungen abbilden, wobei entstehende Kosten abgezogen werden.
Finden wir nun, entweder klassisch oder per Quantum Annealing, ein Matching mit maximaler Summe der Kantengewichte, erfüllt dieses Ergebnis folgende Eigenschaften:
- Da im Matching jeder Knoten aus (V)maximal einmal vorkommt, werden nach unserer Definition von (S) und (D) keine Produktionsstätten überlastet und keine Aufträge ausgeführt, die nicht zur Abdeckung der vorhergesagten Nachfrage dienen.
- Da das Matching die maximal mögliche Summe Kantengewichte hat, entspricht es auch der Zuteilung des Angebots zu Aufträgen aus der Nachfrage mit dem maximal möglichen erzielten Gewinn.
Eine Lösung unseres Assignmentproblems liefert uns also eine optimale Zuteilung der verfügbaren Ressourcen unseres betrachteten Unternehmens in der betrachteten Zeitspanne.
Vom Graphen zum QUBO-Problem
Wir haben uns ausführlich mit dem Assignmentproblem und einer industriellen Beispielanwendung befasst. Jedoch können die Quantum Annealer von D-Wave nicht direkt mit einem graphentheoretischen Optimierungsproblem umgehen, sondern benötigen sehr spezielle Problemformate, die in einer quadratischen Matrix kodiert werden können. Eines dieser Formate ist das Quadratic Unconstrained Binary Optimization-Problem, kurz QUBO.
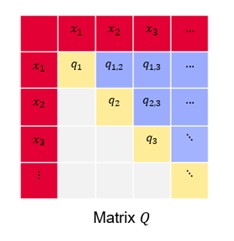
Die formale Definition des allgemeinen QUBO-Problems lautet: $$ minimize/maximize_{x∈{0,1}^k} y= x^T Q_x $$
mit einem Vektor von binären Entscheidungsvariablen x und einer problemspezifischen quadratischen Matrix (Q) mit (k x k) reellen Einträgen [4].
Zu erwähnen ist hier, dass die Maximierungs- und die Minimierungsvariante des Problems äquivalent zueinander sind und durch die Transformation (Q↦ -Q) ineinander umgewandelt werden können. Im Folgenden betrachten wir stets das Minimierungsproblem.
Bevor wir damit anfangen, das Assignmentproblem in diese Form umzuwandeln, verdeutlichen wir zunächst, was die Einträge von im Einzelnen repräsentieren. Eine Ausmultiplizierung der oben eingeführten Definition des QUBO-Problems ergibt folgende Formel: $$ minimize_{x∈{0,1}^k} x^T Qx = minimize_{x∈{0,1}^k} sum_{i=1}^{k} q_ii x_i + sum_{i=1}^{k} q_{ij} x_i x_j $$
Hier kann man erkennen, dass die Einträge von , die auf der Diagonale liegen, jeweils nur mit einer Entscheidungsvariable aus (x) multipliziert werden, während alle anderen Einträge (q_{ij}) mit (i≠j) von (Q) mit zwei Entscheidungsvariablen multipliziert werden. Das QUBO-Problem lässt sich also in einen linearen und einen quadratischen Term aufteilen, um den potenziellen Nutzen von einzelnen Entscheidungen sowie die Zusammenhänge zwischen je zwei Entscheidungen getrennt voneinander betrachten zu können.
Nun können wir uns der tatsächlichen Umwandlung des Assignmentproblems in eine QUBO-Formulierung widmen. Wir erinnern uns an die allgemeine Definition des Assignmentproblems als Graph (G=(V,E)) mit (|E|=m). Um von diesem Graphen zu einem QUBO-Problem zu gelangen, definieren wir zunächst unseren Entscheidungsvektor (x =(x_1,x_2,…,x_m)) mit jeweils einer Entscheidungsvariable (x_{i}∈ (0,1)) für jede Kante in (E). Die zu treffenden Entscheidungen bestehen also darin, welche Kanten des Graphen wir ins resultierende Matching aufnehmen und welche nicht.
Im ursprünglichen Assignmentproblem ist der zu optimierende Wert die Summe aller Kantengewichte im Matching. Dies lässt sich intuitiv durch den linearen Anteil des QUBO-Problems repräsentieren; die Einträge (q_{ii})auf der Diagonale von Q entsprechen also jeweils dem Gewicht der zur Entscheidungsvariable (x_{i} )gehörenden Kante (e_{i}∈E). Zu beachten ist hier, dass wir am Ende ein Minimierungsproblem bekommen wollen; sollte unsere betrachtete Instanz des Assignmentproblems ein Maximierungsproblem sein, müssen wir hier also die negativen Kantengewichte (-w{_e}) für die Diagonaleinträge verwenden.
Die verbleibenden Einträge der QUBO-Matrix (Q), die zum quadratischen Anteil des QUBO-Problems gehören, werden genutzt, um Nebenbedingungen in unsere Zielfunktion zu integrieren. Wir erinnern uns, dass das Assignmentproblem noch die Bedingung enthält, dass die resultierende Kantenmenge ein Matching bildet, also keine zwei Kanten im Ergebnis einen Knoten teilen. Diese Bedingung lässt sich zwar nicht direkt an alle Ergebnisse des QUBO-Problems stellen; sie lässt sich aber so in den quadratischen Anteil des Problems übertragen, dass sie für alle optimalen und annähernd optimalen Lösungen des Problems gilt. Hierfür setzen wir einfach alle Einträge (q_{ij}) mit (i≠j) von (Q), sodass die Kanten zu (x_i) und (x_j) einen Knoten teilen, auf einen hohen, positiven Wert. Die optimale Wahl dieses Strafwerts für die Nutzung von Quantum Annealing ist noch eine offene Frage; er sollte jedoch größer als alle vorkommenden Kantengewichte sein, damit Lösungen, die keinem Matching entsprechen, nicht nur suboptimal, sondern auch klar abgrenzbar von den zulässigen Lösungen sind.
Nun werden noch alle verbleibenden Einträge (q_{ij}) auf 0 gesetzt. Somit ist unsere Transformation des Assignmentproblems in eine QUBO-Formulierung abgeschlossen. Um diese QUBO-Formulierung tatsächlich auf einem Quantum Annealer von D-Wave nutzbar zu machen, müssen wir die QUBO-Matrix (Q) nun noch in eine Obere Dreiecksform bringen. Dies erfordert zwei einfache Schritte [4]:
- Wir ersetzen alle Einträge (q_{ij}) von (Q) mit (i<j) durch (q_{ij}+q_{ji}).
- Wir ersetzen alle Einträge (q_{ij}) von (Q) mit (i>j) durch 0.
Somit haben wir eine vollständige Methode, ein beliebiges Assignmentproblem so umzuformen, dass eine Lösung mit Quantum Annealing oder einer anderen Lösungsmethode für QUBO-Probleme möglich ist.
Weitere Anwendungsmöglichkeiten und Ausblick
Zu Beginn dieses Beitrags haben wir mit dem Demand-Supply-Matching bereits eine in der industriellen Praxis relevante Anwendung des Assignmentproblems kennengelernt. Dies ist jedoch bei weitem nicht das einzige praktisch vorkommende Problem, das als Instanz des Assignmentproblems verstanden werden kann. In der Industrie und außerhalb sind noch viele weitere Anwendungen denkbar, beispielsweise die Zuteilung von (in mittlerer Zukunft potenziell autonomen) Taxis auf Passagiere, die effiziente Aufteilung von Arbeitsschritten auf Arbeitskräfte oder auch die optimale Aufteilung von Büroarbeitsplätzen auf Mitarbeiter.
Es ist außerdem zu betonen, dass die Ergebnisse, die in diesem Beitrag vorgestellt wurden, bisher nahezu ausschließlich theoretischer Natur sind. Die Frage, wie performant die verfügbaren Quantum Annealer mit tatsächlichen Anwendungen sind, bleibt aktuell offen; erste Tests mit einer verhältnismäßig kleinen (40 Kanten im Graphen ≙ 40 Qubits) Modellinstanz des oben zuletzt genannten Anwendungsfalls der Sitzplatzverteilung in einem Bürogebäude ergaben eher enttäuschende Ergebnisse bei einer reinen Nutzung eines Quantum Annealers, allerdings deutlich bessere Ergebnisse bei einer Nutzung des ebenfalls von D-Wave bereitgestellten Hybrid Solver Service, der Quantum Annealing mit klassischen Rechenmethoden kombiniert. Da die genaue Funktionsweise der Hybridmethode leider nicht öffentlich zugänglich ist, ist ein nächster Schritt der Versuch, eine eigene Implementierung für eine ähnlich performante hybride Methode zu entwickeln; ein möglicher Ansatz hierfür ist beispielsweise ein „Iterative Heuristic Solver“, beschrieben von Rosenberg et al. [5].
Zuletzt bleibt noch zu erwähnen, dass, während sich dieser Beitrag ausschließlich mit Quantum Annealing beschäftigt, auch andere Quantentechnologien zur Lösung des Assignmentproblems eingesetzt werden könnten. Eine Implementierung mithilfe des Quantum Approximate Optimization Algorithm, kurz QAOA, ist zum Beispiel auch möglich und könnte ebenfalls erhebliche Vorteile gegenüber klassischen Lösungsmethoden liefern, sobald geeignete Quantencomputer mit ausreichend Qubits zur Verfügung stehen.
Referenzen:
[1] IBM, „IBM Quantum,“ [Online]. Available: https://quantum-computing.ibm.com/services?services=systems. [Accessed 12 07 2021].
[2] D-Wave Systems, „Advantage | D-Wave Systems,“ [Online]. Available: https://dwavesys.com/d-wave-two%E2%84%A2-system. [Accessed 12 07 2021].
[3] R. Duan und S. Pettie, „Linear-Time Approximation for Maximum Weight Matching,“ Journal of the ACM, Bd. 61, Nr. 1, pp. 1-23, 2014.
[4] F. Glover, G. Kochenberger und Y. Du, A Tutorial on Formulating and Using QUBO Models, arXiv:1811.11538 [cs.Ds], 2019.
[5] G. Rosenberg, M. Vazifeh, B. Woods und E. Haber, „Building an Iterative Heuristic Solver for a Quantum Annealer,“ Computational Optimization and Applications, Bd. 65, Nr. 3, pp. 845-869, 2016.




Um einen Kommentar zu hinterlassen müssen sie Autor sein, oder mit Ihrem LinkedIn Account eingeloggt sein.