Quantum data communication protocols are theoretically secure, aren’t they? But wait, they involve classical bits. Quantum nodes use classical hardware and software. Quantum storage is sensitive to environmental disturbances, that may have malicious origins. These reasons are good enough to motive the need to protect quantum data communications, in particular when quantum data disclosure or loss of integrity may have high impact on their owner. How can quantum data be protected during communications? This article examines this question and outline some of the current answers.
Quantum data protection is an emerging area that has been a subject of recent attention by researchers. In this article, two key aspects are discussed in details: integrity and confidentiality. Authentication protects quantum data integrity, i.e., alteration by an adversary. Cryptographic techniques protect the confidentiality of information represented in quantum data from non-authorized access. We review the principal features of quantum cryptographic schemes that have been created to achieve authentication and confidentiality of quantum data. We discuss how they can be applied to protect quantum data communications and networking. Firstly, we introduce key quantum information concepts.
Quantum state
In the quantum information model, the unit of information is called the quantum bit, or qubit. In contrast to a classical bit, a qubit can be simultaneously in states zero and one. In fact, a qubit is in a superposition of states zero and one. This superposition condition can be interpreted as the association of a probability p of reading a qubit into value zero, and 1-p of reading it into a one (Fig. 1).
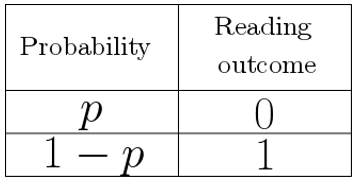
A qubit is in the zero-one superposition condition until it is read, which outcome is a zero or a one. In contrast to a classical bit that can be read several times, a qubit can be read only once. Reading is destructive. Furthermore, it is impossible to make a perfect copy of a qubit.
Qubits are interesting because they can be composed together to build complex quantum states. They can also interact together and be entangled. They can represent problems that involve an enormous amount of combinations in a very compact way, at least conceptually. This capability is exploited by the Shor’s quantum algorithm for efficient integer factorization. A quantum state is a composition of n qubits. There are 2^n possible reading outcomes with respective probabilities p_0,…,p_(2^n-1) (Fig. 2).
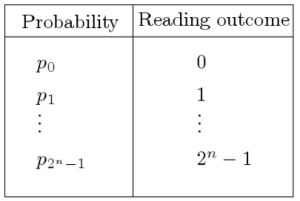
A for a single qubit, a quantum state be read only once. Reading is destructive. In addition, it is impossible to make a perfect copy of a quantum state.
Quantum entanglement
Qubits may be entangled, that is, related together such that they read in a coherent way. This means that some of the reading outcomes are made more probable than others. Besides, some reading outcomes can be made entirely non-probable. Entanglement is a key property of quantum distributed computing, communications and networking because the phenomenon works across distances. That is, two entangled qubits may be physically separated by an arbitrary long distance. However, despite their physical separation, the two individual qubits behave as if they were a single entity. The measurement of one qubit determines the outcome of the measurement of the other qubit.
Quantum transformation
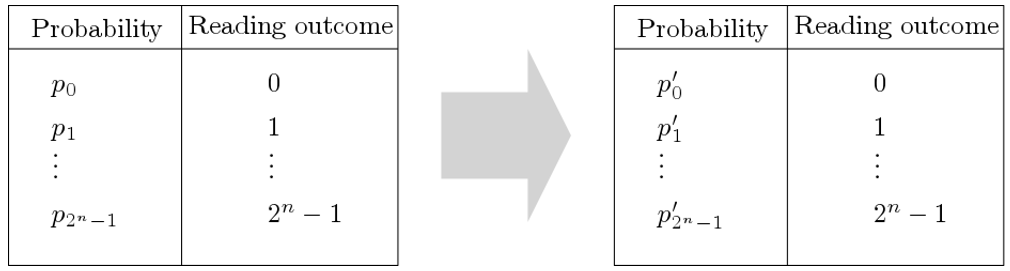
In the quantum world, computing takes the form of transformations of quantum states. The art of quantum programming consists of translating an idea into the right transformation(s). A transformation can be on a single qubit or on a whole quantum state. Not any transformation is permitted, which makes quantum programming a bit tricky. A transformation is valid solely if it reassigns new probabilities p_0^‘,…,p_(2^n-1)^‘ to the reading outcomes of the quantum state (Fig. 3).
Quantum communications and networking
Quantum data communications and networking aim at supporting applications that need the transfer of quantum states from one network node to another, e.g., for the purpose of distributed quantum computing. It is foreseen that quantum teleportation and quantum repeaters will play key roles in future quantum networks.
Quantum teleportation. Teleportation is a point-to-point protocol devised to transfer a qubit from one location to another, i.e., a source and a destination. It builds upon pre-shared entanglement between the source and destination. It is assumed that they have the capability of long-term storage of pre-shared entangled qubits. The entangled qubits can be obtained at network setup time. The parties must also be able to exchange classical bits. The transfer of every qubit requires the transfer of two classical bits.
Quantum repeater. For quantum networking, the use of quantum repeaters is envisioned for the end-to-end transfer of quantum states. Quantum repeaters leverage entanglement swapping, possibly together with error correction, to achieve multi-hop communications. Using pre-established node-to-node entanglement, entanglement swapping establishes an entangled qubit between a source and a destination. This end-to-end entanglement is used to transfer a qubit from the source to the destination. Entanglement swapping is conceptually similar to teleportation. The swap of every qubit requires the transmission of two classical bits. A coordination protocol between participating nodes is also required. On a multi-hop network, routing of a quantum state requires several swaps and classical bit transmissions.
Need for quantum data protection
When alteration and disclosure have impact, integrity and confidentiality of quantum data need to be protected. Quantum computing, communications and networking use classical hardware and software. Classical hardware and software can be compromised. Hence, quantum hardware and software are vulnerable to all classical attacks. They may lead to disclosure of quantum data. An attack can disturb quantum states in a random way. The state loose its authenticity. Teleportation of quantum states and quantum repeaters use classical qubit communications to implement their logic. When they are attacked, teleported or swapped qubits may lose their integrity. Quantum data protection builds upon the science of quantum cryptography.
Quantum data integrity protection
Authentication is a data integrity protection mechanism. Authentication aims at demonstrating that quantum data has not been altered by an adversary during the transit between a source and a destination. Authentication is achieved using a data signature mechanism.
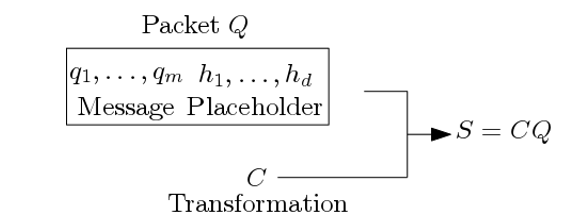
The quantum authentication procedure is based on a shared secret. The sender-side authentication procedure is schematically outlined in Fig. 4. A quantum packet Q comprises a m-qubit message q_1,…,q_m and a placeholder for a quantum signature made of d qubits h_1,…,h_d. The number d is a security parameter. The larger the better. The shared secret is a quantum operator C is used to transform the packet Q into a quantum state S. The transformation, S=CQ, computes the quantum signature and loads it into the placeholder.
There are important aspects to highlight. The transformation C is chosen with key mathematical properties. It has an inverse transformation C^†. That means that when S is integrally forwarded to the destination, the application of C^† to the received content restores the original quantum state. An attack to the integrity of a quantum state translates to the application of some quantum transformation P. The transformation C is selected such that P is mapped to a transformation that has an effect on the qubits in the signature. Hence, in the attack is detectable.
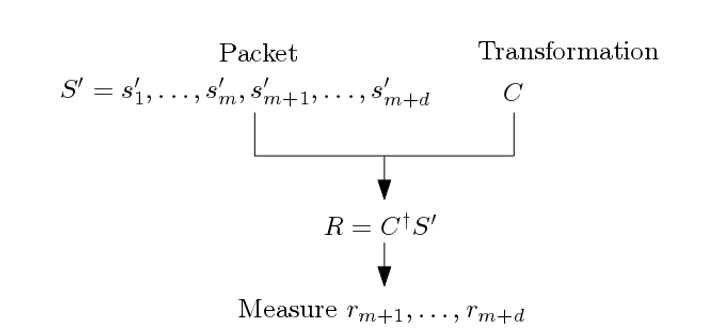
The quantum packet S is forwarded to the destination, using teleportation or a network of quantum repeaters. There is a risk that the quantum packet is altered by an adversary because quantum communications and networking require as well the transmission of auxiliary classical bits and classical control software, such as operating systems. At the destination, the receiver gets a quantum S‘ that may or may not correspond to S. When the quantum state has not been altered, S‘ is equal to S. This is verified by an inspection of the signature. Fig. 5, the receiver gets a quantum packet S‘ consisting of a m+d-qubit state s_1^‘,…,s_m^‘,s_(m+1)^‘,…,s_(m+d)^‘. It applies to S‘ the inverse transformation C^† to obtain the quantum state R, i.e., R is equal to C^† S‘. The d rightmost qubits of R are r_(m+1),…,r_(m+d). Measurement of qubits r_(m+1),…,r_(m+d) should yield d zeros. The original quantum message q_1,…,q_m is in qubits r_1,…,r_m. Otherwise, the quantum authentication procedure failed and the message has been compromised and should be rejected.
Quantum data confidentiality protection
The goal of confidentiality is to insure the secrecy of data during the transport from a source to a destination. Confidentiality is achieved by encrypting data. Quantum cryptographers have developed encryption techniques specifically for quantum data that may be used to protect the confidentiality of information during communication and transit over a network. There are two forms of encryption: symmetric and symmetric. We discuss the symmetric form first.
Symmetric quantum data encryption
Symmetric encryption means that the sender and receiver share a common secret key. The symmetric encryption procedure is based on a shared n-bit classical key k and a one-way hash function f. An output of f does not reveal any information about its input. The hash function takes as arguments the key k and a random index i. It returns a value used as an index to select a transformation. The value i plays the role of initialization vector. A repeated usage of key k does not allow an adversary to infer a relationship between encrypted messages. The symmetric key k is a secret shared by the sender and receiver.
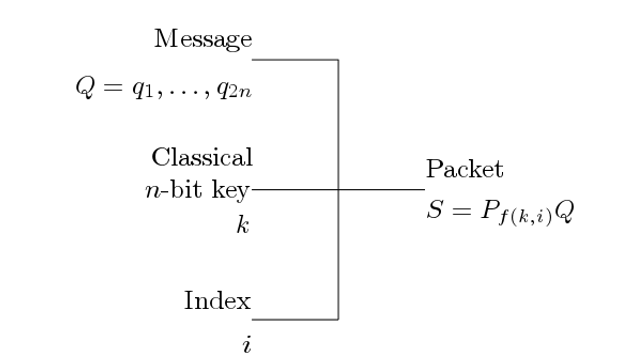
Fig. 6 pictures the encryption procedure performed by the sender. The sender has a message consisting of 2n qubits q_1,…,q_2n. Given key k and index i, the result of the evaluation of the hash function f(k,i) is used as an index to determine a quantum transformation P_(f(k,i)). The source computes S equal to the product P_(f(k,i)) Q and sends S and i.
In this scheme, when an adversary succeeds reading the quantum state S, before it reaches its destination, information is concealed due to the presence of transformation P_(f(k,i)). The adversary may try to guess what f(k,i) is. In contrast to classical cryptanalysis, due to the fact that quantum state reading is destructive and impossibility to copy, the adversary has only one trial. Hence, a brute-force attack cannot be perpetrated. The transformation P_(f(k,i)) is chosen such that it has the self-inverse property. Assuming that S and i are correctly delivered to the final destination, a second application of transformation P_(f(k,i)) to S restores the initial state Q.

Fig. 7 pictures how cipher text is decrypted. The destination owns the secret key k and receives a quantum state S‘ consisting of the qubits 〖s’〗_1,…,〖s’〗_2n and index i‘. Let P_(f(k,i‘)) be the transformation determined by the index f(k,i‘). To obtain the plain text, the transformation P_(f(k,i‘)) is applied to S‘, that is, the received plaintext Q‘ is equal to P_(f(k,i‘)) S‘.
Asymmetric quantum data encryption
Asymmetric encryption means that the sender uses a public encryption key and the receiver uses the corresponding private decryption key. The asymmetric key encryption procedure uses a n-bit classical public key i. The public key determines an indexed permutation function f_i. The indexed function f_i is chosen such that it has the one-way and trapdoor properties. The latter means that, given an output f_i (x) and a trapdoor value t, the input x can be determined easily. Using function f_i, a function h that has the hard-core property is constructed to generate pseudo-random values. The value returned by an invocation of function h is used to determine the index of a transformation. The hardcore property means that given the result of f_i (x), it is difficult to determine h(x). The trapdoor value t plays the role of private key. It is used to resolve the inverse permutation of f_i (x), denoted by g_i (x).

Asymmetric key quantum data encryption is outlined in Fig. 8. Let Q be a quantum state representing a message consisting of the n qubits q_1,…,q_█( @n). A value d is selected at random such that f_i (d) is not null. The hardcore of d, i.e., h(d) is used as an index to determine a transformation P_(h(d)). The source sends the quantum state S equal to the product P_(h(d)) Q together with the hash value f_i (d).
We have conditions similar to quantum symmetric encryption, but not exactly the same. When an adversary succeeds reading the quantum state S before it reaches its destination, information is concealed due to the presence of transformation P_(h(d)). Using the hash value f_i (d), the adversary may try to guess what the random value d is and calculate the hard-core value h(d), perpetrating a brute-force attack, i.e., a search for the trapdoor value t. Because it is single read and impossible to copy, a chosen transformation P_(h(d)) can be tried only once on a quantum state. The transformation P_(h(d)) is chosen such that it has the self-inverse property. Assuming that S and f_i (d) are correctly delivered to the final destination, a second application of transformation P_(h(d)) to S restores the initial state Q.

The decryption procedure uses a n-bit classical private key, i.e., the trapdoor value t (Fig. 9). The destination receives a quantum state S^‘ made of 2n qubits s_1^‘,…,s_2n^‘, representing an encrypted message, and a hash value v. Using the trapdoor value t, the inverse permutation function g_i of function f_i is used to determine d equal to g_i (v) and calculate the hardcore h(d). The receiver applies the transformation P_h(d) to S^‘ to obtain the n-qubit plain text quantum state Q‘.
Further readings
Quantum data communication protection and encryption are relatively news topics. The goal of this article was to demonstrate their relevance and outline some of the main ideas developed by researchers. Visit the web page of the author for more readings and relevant reference material (carleton.ca/scs/people/michel-barbeau).



Um einen Kommentar zu hinterlassen müssen sie Autor sein, oder mit Ihrem LinkedIn Account eingeloggt sein.