Quantum computing is one of the hottest topics in computer science. With D-Wave Systems releasing the first commercially available quantum annealer in 2011 [1], there is now the possibility to develop practical quantum algorithms for solving complex optimization problems. In this article a hybrid quantum solution method for the Capacitated Vehicle Routing Problem is presented.
1. Introduction
Optimization problems can be found in many application domains, be it economics and finance [2], logistics [3], or healthcare [4]. Their high complexity engaged researchers to develop efficient methods for solving these problems [5].This article regards the Capacitated Vehicle Routing Problem (CVRP), an NP-hard optimization problem that plays a major role in common operations research and is excessively studied since its proposal in 1959 [6]. It generalizes and combines many important research scenarios like intelligent transportation, autonomous driving or automation and optimization. The classic CVRP (see Figure 1) can be described as the problem of designing optimal routes from one depot to a number of geographically scattered customers subject to some side constraints. It can be formulated as follows:
Let G = (V, E) be a graph with V = {1, …, n} being a set of vertices representing n customer locations with the depot located at vertex 1 and E being a set of undirected edges. With every edge (i, j) ∈ E, ij a non-negative cost cij is associated. This cost may, for instance, represent the (geographical) distance between two customers i and j. Furthermore, assume there are m vehicles stationed at the depot that have the same capacity Q. In addition, every customer has a certain demand q. The CVRP consists of finding a set of vehicle routes such that
- each customer in V {1} is visited exactly once by exactly one vehicle;
- all routes start and end at the depot;
- the sum of customer demand within a route does not exceed the vehicles’ capacity;
- the sum of costs of all routes is minimal given the constraints above;
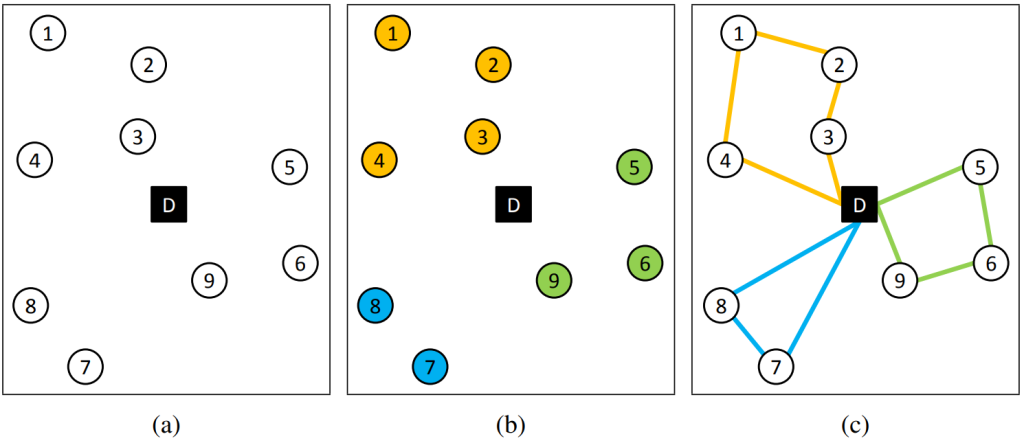
In this article an intuitive way to split the CVRP into smaller optimization problems by taking advantage of a classical 2-phase-heuristic [8] is presented (see Figure 1). The heuristic divides the CVRP into two phases, the clustering phase and the routing phase. The clustering phase itself can easily be computed by a classical clustering algorithm (e.g. modified k-means algorithm), which tries to group the customers into capacity restricted clusters. Doing this, the Euclidean distance between customers assigned to a cluster should be minimized. The routing phase can be represented by the well-known NP-hard Traveling Salesman Problem (TSP) [9]. Thus, the minimal tour in which all customers of a cluster are visited once is sought. Doing this, the tour starts and ends in one place, i.e. the depot. In Figure 1 a CVRP example with the 2-phase-heuristic is visualized. First the customers are grouped into clusters (b) before efficient vehicle routes in each cluster are calculated (c).
D-Wave’s quantum annealing hardware is known to solve a specific optimization problem called a quadratic unconstrained binary optimization (QUBO) problem [10]. QUBO is a unifying model which can be used for representing a wide range of other combinatorial optimization problems, to which also the TSP belongs.
In this article a hybrid method based on the 2-Phase-Heuristic to solve the CVRP using a quantum annealer is proposed. While the clustering phase is computed classically, the routing phase, i.e. the TSP, is solved on the quantum hardware.
2. Quantum annealing on D-Wave processor
The most obvious difference between quantum and classical informatics is the so called state principle. Quantum particles can reside in multiple states, such as having different locations, energies, or move in different speeds. Additionally, in quantum mechanics, such particles adopt not only one, but multiple states at the same time. This behavior can be illustrated by thinking of quantum particles as waves that can overlap, extinguish or amplify one another, just as known from classical physics. One property of quantum bits (qubits) is called superposition and describes the ability to reside in two states simultaneously, hence be in the state 0 and 1 at the same time [11]. The difference between the two computing systems gets even more clear with multiple (qu)bits: A classical computer can represent 2n different numbers with n bits, but only save one of them at a time. A quantum computer, however, can represent the same amount of numbers with an equally amount of quantum bits, all at the same time [12]. Another property that is not consistent with our classical view on physics is called entanglement. The manipulation of one entangled bit can affect the measurement of another bit. More interestingly, this behavior does not require the two qubits to be in direct contact, and is therefore the basis of research concerning quantum teleportation [12].
Using these fundamental quantum effects, one hopes for solving complex problems in a faster way than classical computation does. However, for solving optimization problems like the TSP on D-Wave’s quantum annealing hardware the problem has to be formulated as a quadratic unconstrained binary optimization (QUBO) problem [10], which is one of two input types acceptable by the machine (alternative: the Ising model [13]). The functional form of the QUBO is:
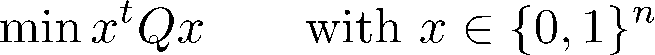
with x being a vector of size n with binary variables, and Q being an n×n real-valued matrix describing the relationship between the variables. Given matrix Q, the annealing process tries to find binary variable assignments to minimize the objective function stated above. The metaheuristic quantum annealing itself, seeks for the minimum of the optimization function, which corresponds to the best solution of the defined optimization problem.
3. Hybrid solution method
The classical distance based clustering phase, in which every customer is assigned to a vehicle cluster considering the capacity constraint, is straight forward. Thus, the focus in this section is on the mapping of the TSP to the QUBO formulation. The TSP tries to find the shortest tour (starting and ending at the depot) between the customers of a cluster. In [14] the mathematical QUBO problem (respectively Ising Model, which is mathematically equivalent) for the TSP is stated:
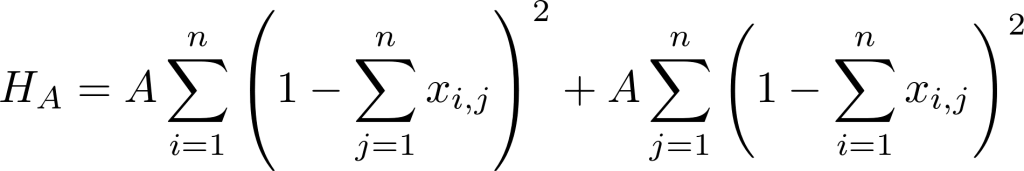
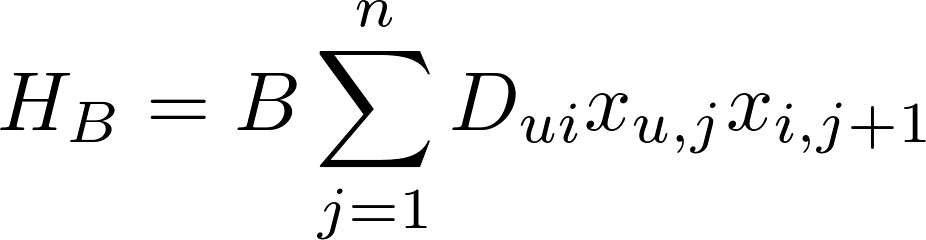
HA and HB describe the energies of the underlying problem, for which the configuration with the lowest corresponding energy is sought. The binary variable xi,j is 1 if the customer with index i is located at position j in the tour. The first term (constraint) of HA requires that each customer must occur only once in the cycle, while the second term of HA enforces that each position in the cycle must be assigned to exactly one customer. This defines the order of the customers within the tour. The squared differences of these terms ensure that exactly one customer has a unique position in the tour. Otherwise, a high penalty value A would be added to the solution energy, which states the solution itself as suboptimal or rather invalid (see example below). The term HB represents the objective function of the TSP in which Dui is the Euclidean distance between the customer u and i. Thus, the minimization function sums all costs of the edges between successive customers. The total solution for the TSP QUBO problem is then composed of the energies: H = HA + HB
Example (Regard first constraint of HA):
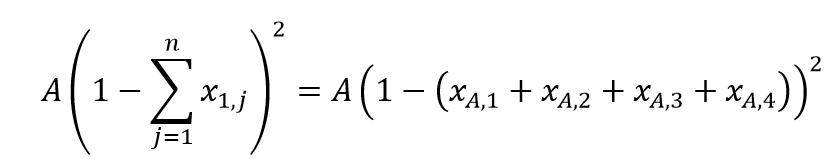
Assume finding a tour between 4 customers. There are four possible positions of customer A in the tour (A1, A2, A3, A4). These position-to-customer-combinations are represented by the binary variable xij and states that customer i has the position j in the tour. If xA1 = 1, customer A was assigned position 1 in the tour. Under the premise that customer A is fixed, sum up all binary variables xAj. These leads to various cases:
- No position was assigned to customer A:
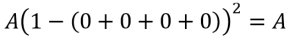
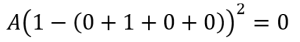
3. Two positions (1, 3) were assigned to customer A:
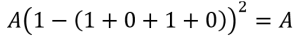
As one can see, the best case – with the lowest energy – is in case 2, where exactly one position is assigned to customer A. This is also the only valid solution. In the other cases (also in case 4 and 5, which were omitted) the penalty value A is added on top of the system energy, which defines a solution as invalid. The second constraint of HA can be regarded analogously.
4. Conclusion
In this article, a hybrid approach for solving the capacitated vehicle routing problem (CVRP) using D-Wave’s quantum annealing hardware was provided. The most important step was to find an intuitive way to map this optimization problem to a QUBO problem that could then be embedded on the quantum annealer. Doing this, the classical 2-phase-heuristic has been used, which enables to divide the complex problem into a clustering phase as well as a routing phase. The solution method was tested and compared regarding the solution quality as well as the computational time. The results can be found in [7].
We showed that the hybrid approach was able to compete with other classical construction and 2-phase-heuristics and in some cases even surpass them with regard to solution quality. However, it should be mentioned that there are other solution methods like metaheuristics, which provide a better solution with regard to some of the used benchmark datasets.
The computational time of this solution method must be considered differentiated. Due to the currently limited number of available qubits on the D-Wave processor, the tool QBSolv must be used for large QUBO problem instances. This tool makes it possible to split the QUBO into smaller subQUBOs and place them one after the other on the quantum annealer. However, this hybrid solution option involves certain latency and waiting times which lacks the hoped acceleration of the computational time compared to the classical option. However, the real solution time for an embeddable QUBO problem on the D-Wave quantum annealer is located in the range of microseconds.
At the 2018 D-Wave Qubits Europe users conference D-Wave provided an outlook about the future hardware directions of quantum annealing. They stated that the connectivity and the number of qubits on D-Wave machines will immensely rise over the next years [15]. This news give hope that in the future D-Wave’s quantum annealers are more suitable for these kind of optimization problems and a shorter total computation time can be achieved.
References:
[1] https://www.dwavesys.com/news/d-wave-systems-sells-its-first-quantum-computing-system-lockheedmartin-corporation
[2] Black, F. and Litterman, R. (1992). Global portfolio optimization. Financial analysts journal , 28–43
[3] Caunhye, A. M., Nie, X., and Pokharel, S. (2012). Optimization models in emergency logistics: A literature review. Socio-economic planning sciences 46, 4–13
[4] Cabrera, E., Taboada, M., Iglesias, M. L., Epelde, F., and Luque, E. (2011). Optimization of healthcare emergency departments by agent-based simulation. Procedia computer science 4, 1880–1889
[5] Papadimitriou, C. H. and Steiglitz, K. (1998). Combinatorial optimization: algorithms and complexity (Courier Corporation)
[6] Dantzig, G. B. and Ramser, J. H. (1959). The truck dispatching problem. Management science6, 80–91 [6] Laporte, G. (1992). The vehicle routing problem: An overview of exact and approximate algorithms. European journal of operational research 59, 345–358
[7] Feld, S., Roch, C., Gabor, T., Seidel, C., Neukart, F., Galter, I., … & Linnhoff-Popien, C. (2018). A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer. arXiv preprint arXiv:1811.07403.
[8] Laporte, G. and Semet, F. (2002). Classical Heuristics for the Capacitated VRP, chap. 5. 109–128. doi:10.1137/1.9780898718515.ch5
[9] Lawler, E. L. (1985). The traveling salesman problem: a guided tour of combinatorial optimization. Wiley-Interscience Series in Discrete Mathematics
[10] Boros, E., Hammer, P. L., and Tavares, G. (2007). Local search heuristics for quadratic unconstrained binary optimization (qubo). Journal of Heuristics 13, 99–132
[11] McGeoch, C. C. (2014). Adiabatic quantum computation and quantum annealing: Theory and practice. Synthesis Lectures on Quantum Computing 5, 1–93
[12] Homeister, M. (2008). Quantum Computing verstehen. Friedr. Vieweg & Sohn Verlag, 2
[13] Glauber, R. J. (1963). Time-dependent statistics of the ising model. Journal of mathematical physics 4, 294–307
[14] Lucas, A. (2014). Ising formulations of many np problems. Frontiers in Physics 2, 5
[15] https://www.dwavesys.com/sites/default/files/mwj_dwave_qubits2018.pdf



Um einen Kommentar zu hinterlassen müssen sie Autor sein, oder mit Ihrem LinkedIn Account eingeloggt sein.